Размещения с повторениями

Размещениями с повторениями элементов n различных типов по т называются их последовательности из т элементов, отличающиеся друг от друга самими элементами или их порядком. При этом возможно и т≤ n, и т>n, поскольку допускается повторение элементов в последовательности из т элементов.

Пример. Размещения с повторениями из 3 элементов а, b и с по 2: аb, bа, ас, са, bс, сb, аа, bb, cc.

Число всех возможных размещений из га различных элементов по т (обозначается 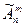) есть 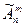= n^m.

Действительно, в последовательности из т элементов n различных типов имеется т позиций. Поскольку элементы в разных позициях могут быть одинаковыми, то элемент, находящийся в 1-й позиции, может быть выбран любым из n типов, элемент во 2-й позиции также может быть выбран любым из n типов и т.д. Наконец, элемент в m-й позиции может быть также выбран любым из n типов. Тогда, по правилу умножения, число последовательностей из m элементов n возможных различных типов с повторениями или число размещений с повторениями есть

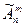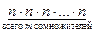= = n^m.

Для примера размещений с повторениями из 3 элементов а, b и с по 2 имеем 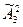=3² =9.

Решением задачи 4 является 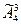=4³ =64 варианта различных 3-буквенных слов-кодов, составленных из 4 букв алфавита, для коди­рования аминокислот.