Различные виды прямой
| Note 1 | В математике понятие «точка», «прямая», «плоскость» – является первичным и через более простое понятие не определяется. |
1. 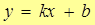 – уравнение прямой с угловым коэффициентом;
– уравнение прямой с угловым коэффициентом;
2. 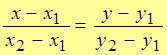 – уравнение прямой, проходящей через две точки;
– уравнение прямой, проходящей через две точки;
3. 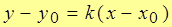 – уравнение пучка прямых;
– уравнение пучка прямых;
4. 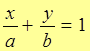 – уравнение прямой в отрезках;
– уравнение прямой в отрезках;
5.  – общее уравнение прямой;
– общее уравнение прямой;
6.  – нормальное уравнение прямой.
– нормальное уравнение прямой.

1. 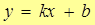 .
.
Пусть на плоскости задана д.п.с.к. X0Y. Пусть L – прямая, проходящая под углом α к оси 0Х и отсекающая отрезок b на оси 0Y. Пусть tgα=k. Пусть т. 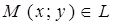 .
.
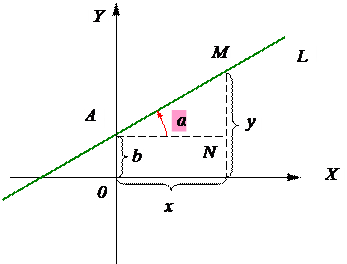
Из прямоугольного треугольника ΔAMN 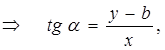 учитывая, что
учитывая, что 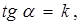 получим
получим 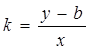 или
или 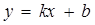 ч. т. д.
ч. т. д.
2. 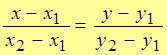 .
.
Пусть прямая L принадлежит плоскости с д.п.с.к. X0Y. Пусть две «фиксированные» точки 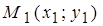 и
и 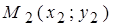 принадлежат прямой L. Пусть т.
принадлежат прямой L. Пусть т. 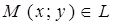 – ее «текущая» точка.
– ее «текущая» точка.
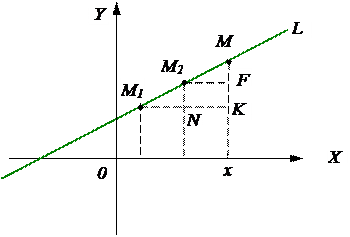 |
Из подобия 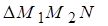 ~
~ 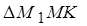 ~
~ 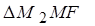 следует, что
следует, что
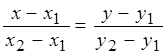 , ч. т. д.
, ч. т. д.
3. 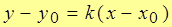 .
.
Пусть прямая L принадлежит плоскости с д.п.с.к. X0Y. Пусть «фиксированная» т. 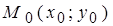 и «текущая» т.
и «текущая» т. 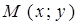 принадлежат прямой L. Пусть α – угол между прямой L и осью 0Х.
принадлежат прямой L. Пусть α – угол между прямой L и осью 0Х.
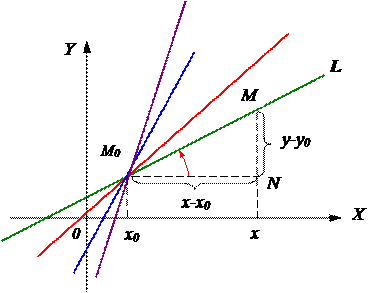 |
Из прямоугольного треугольника ΔM0MN 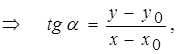 или
или 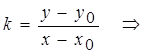
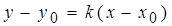 . Если угловой коэффициент k считать переменной величиной, то получим бесконечное множество прямых, проходящих через т. М0 .
. Если угловой коэффициент k считать переменной величиной, то получим бесконечное множество прямых, проходящих через т. М0 .
4. 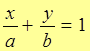
Пусть прямая L принадлежит плоскости с д.п.с.к. X0Y и отсекает отрезок а на оси 0Х и отрезок b на оси 0Y. Пусть координаты этих точек A(a;0), B(0;b).
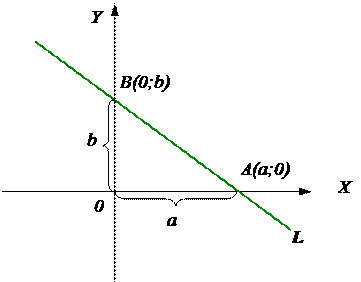 |
Составим уравнение прямой, проходящей через т. А и т. В.
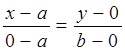 , откуда
, откуда 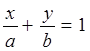 , ч. т. д.
, ч. т. д.
5.  .
.
Пусть x, y – переменные величины; A, B, C – числа (const).
Докажем, что на плоскости с д.п.с.к. X0Y это уравнение описывает некоторую прямую L.
Действительно, пусть 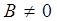 , тогда
, тогда 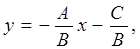 или, обозначая
или, обозначая 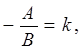
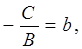 получим
получим 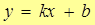 – уравнение прямой с угловым коэффициентом (см. 1).
– уравнение прямой с угловым коэффициентом (см. 1).
Пусть 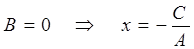 – прямая параллельна оси 0Y.
– прямая параллельна оси 0Y.
Пусть 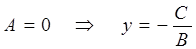 – прямая параллельна оси 0X.
– прямая параллельна оси 0X.
Пусть 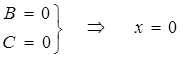 – уравнение оси 0Y.
– уравнение оси 0Y.
Пусть 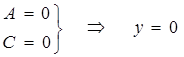 – уравнение оси 0X.
– уравнение оси 0X.
6.  .
.
Пусть прямая L принадлежит плоскости с д.п.с.к. X0Y. Пусть p - расстояние от начала координат до прямой L. 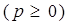 .
.
Пусть т. 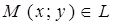 – «текущая» точка прямой L.
– «текущая» точка прямой L.
Пусть r – расстояние от начала координат до т. М.
 Пусть т.
Пусть т. 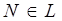 и
и 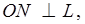 тогда
тогда 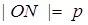 .
.
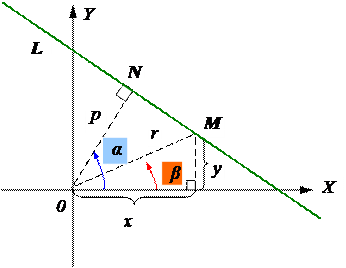
Пусть угол между ON и осью 0Х равен α, а угол между OM и осью 0Х равен β.
Из прямоугольного треугольника ΔONM следует, что
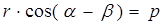 ,
,
или (применяя формулы тригонометрии)
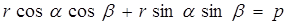 .
.
Учитывая, что 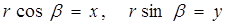 , получим
, получим
 , ч. т. д.
, ч. т. д.
| Note 2 | Дома или на п/з из каждого уравнения 1 – 6 получить остальные уравнения 1 – 6. |
Дата добавления: 2015-08-20; просмотров: 703;
