Прямая геодезическая задача

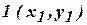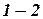Сущность прямой геодезической задачи (рис. ): по известным координатам точки линии , дирекционному углу этой линии 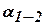и ее горизонтальному проложению 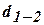требуется определить координаты точки .

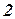Проведя через точк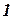и и 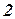линии, параллельные координатным осям, получим прямоугольный треугольник 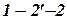, в котором известны гипотенуза 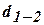и острый угол 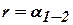. Катеты этого треугольника есть приращения координат 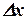и , которые могут быть получены по формулам:

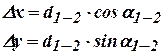(13.18)

Контроль:

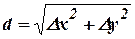. (13.19)

Следует помнить, что в общем случае знаки приращений координат зависят от четверти, определяемой дирекционным углом заданного направления (см. табл.13.1).

Тогда координаты искомой точки 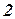определяются по формулам

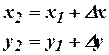(13.20)

или

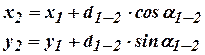(13.21)

Приращения координат и координаты искомой точки вычисляются с точностью, соответствующей точности измерения горизонтальной длины линии.