Основные величины, измеряемые в геодезии

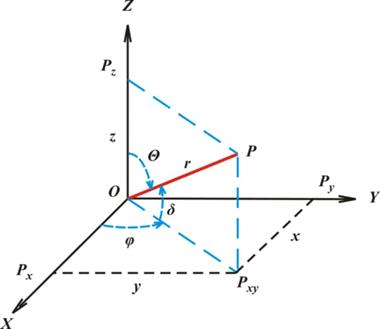
Одной из главных задач геодезии является определение пространственного положения одних точек относительно других. Но поскольку измерения выполняются не сразу все одновременно, а последовательно, одно за другим, то правильнее будет сказать, определение пространственного положения одной точки относительно другой. Если в качестве одной из указанных двух точек принять точку стояния наблюдателя, то относительно пространственного положения второй точки можно сказать, что она находится выше или ниже первой точки, левее или правее какого-то выбранного ориентирного направления, ближе или дальше какой-либо третьей точки, лежащей на одной линии с точкой стояния и наблюдаемой точкой. Все это есть не что иное, как описание пространственного положения произвольно выбранной точки в пространственном варианте полярной системы координат, связанной с точкой стояния наблюдателя. Такая система называется сферической и показана на рис. 15.1

Рис. 15.1 – Сферическая и пространственная прямоугольная системы координат

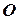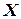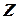На этом рисунке точка - это точка стояния наблюдателя, т.е. полюс, а оси и - полярные оси. Точка 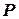- точка, для которой определяется ее пространственное положение относительно точки .

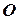Возникает естественный вопрос: как ориентировать в пространстве полярную ось?

Особенностью физического пространства, в котором мы живем на планете Земля, является то, что в каждой точке поверхности Земли, ее недр, а также воздушной и водной оболочки, есть выделенное направление – отвесная линия. Именно с отвесной линией связана вся наша жизнь. Есть у отвесной линии и ее производная – горизонтальная плоскость, которая перпендикулярна отвесной линии.

Поэтому сориентируем ось 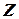таким образом, чтобы она совпала с отвесной линией в точке 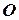. Тогда ось 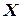займет горизонтальное положение.

Положение точки 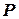в сферической системе координат описывает радиус-вектор 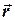. Расстояние от точки 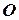до точки 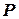равно модулю вектора 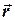. Положение же самого вектора 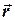описывается двумя углами: азимутальным углом 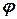между полярной осью 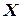и проекцией вектора 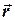на горизонтальную плоскость, и углом наклона 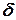, если этот угол отсчитывать от проекции вектора 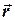на горизонтальную плоскость до самого вектора, либо зенитным расстоянием (углом) 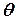, если его отсчитывать от второй полярной оси 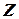, т.е. отвесной линии, до самого вектора .

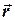Это значит, что для описания пространственного положения одной точки относительно другой, необходимо знать 3 величины: 2 угла, один в горизонтальной плоскости, второй в вертикальной, и наклонное расстояние. Зная указанные величины легко можно перейти к пространственным прямоугольным координатам точки 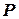, которые могут быть вычислены в случае зенитного угла как

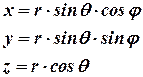, (15.1)

либо в случае угла наклона как

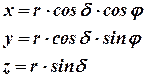. (15.2)

Если внимательно посмотреть на рис. 15.1, то можно заметить, что величина 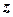, численно равна расстоянию 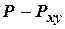, которое показывает расстояние от точки 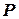до ее проекции на горизонтальную плоскость. Но поскольку горизонтальная плоскость в данном случае проведена через точку 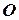, то эта плоскость может считаться уровенной поверхностью. А тогда отрезок 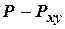будет ни чем иным, как превышением точки 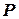над точкой 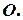Расстояние 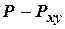может быть определено не только в результате вычислений по формулам 15.1 и 15.2, но может быть измерено и непосредственно.

Все это означает, что поскольку при определении пространственного положения точек участвуют только углы и длины, то основными измеряемыми величинами в геодезии являются угловые и линейные величины. Причем среди угловых величин необходимо различать горизонтальные углы и вертикальные углы. Но если есть измеряемые величины, то должны быть и приборы для измерения этих величин. Вот к рассмотрению этих приборов мы и приступим.