Дисперсия. Математическое ожидание является важнейшей числовой характеристикой случайной величины
Математическое ожидание является важнейшей числовой характеристикой случайной величины. Но полностью случайную величину оно не характеризует.
Пример:
Найти математическое ожидание, если
| x | -10 | -6 | -2 | |||||
| Р | 1/6 | 1/8 | 1/4 | 1/16 | 1/4 | 1/16 | 1/8 | 1/16 |
| y | -2 | -1 | ||||||
| Р | 1/4 | 1/4 | 1/16 | 1/16 | 1/8 | 1/8 | 1/8 |
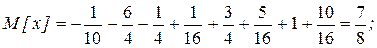
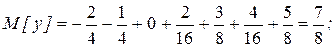
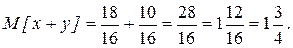
Во втором распределении значения случайной величины компактно сосредоточены около математического ожидания. Зная только среднее значение случайной величины нельзя представить себе расположение значений случайной величины. Если значения случайной величины рассеяны вдоль числовой оси, то математическое ожидание играет роль центра этого рассеяния, т.е. нужна еще одна числовая характеристика, показывающая как сильно рассеяны значения случайной величины вокруг этого центра. Дисперсия и характеризует рассеяние значения случайной величины около ее математического ожидания.
Пусть x – случайная величина математическое ожидание которой известно M[x], в качестве новой случайной величины рассмотрим разность
(x-M[x])
Т.е. эту разность называют отклонением случайной величины x от ее математического ожидания.
Определение: Дисперсией или рассеянием случайной величины x называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, т.е
D[x]=M[(x-M[x])2] (1)
Если D - сравнительно малое число , то в этом случае значения случайной величины близки к ее математическому ожиданию. Если же дисперсия большое число, то значения сильно рассредоточены, рассеяны около математического ожидания.
Преобразуем формулу (1)
D[x]=M[х2-2×х×М[х]+М[х]]=M[x2]-2×M[x]×M[x]+m[x]2;
D=М[х2]-М2[х] (2)
Пусть х – непрерывная случайная величина, плотность распределения ее f(x) и математическое ожидание M[x], то для дисперсии существует такая формула:
 (3)
(3)
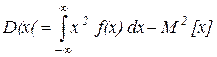 (4)
(4)
Дата добавления: 2015-08-14; просмотров: 717;
