Дисперсия в волокнах

В оптических линиях связи широко используют кодово-импульсную модуляцию (КИМ). В этом случае информационный сигнал представляет собой последовательность импульсов, которая в закодированном виде содержит передаваемое сообщение. В результате дисперсии происходит уширение импульса (рис. 84.1, а). Если дисперсия велика, то два последовательных импульса могут перекрываться (рис. 84.1, б) и получатель сигнала примет их за один, а это означает искажение передаваемой информации. Для предотвращения ошибок следует увеличить интервал между соседними импульсами, т. е. уменьшить частоту следования импульсов (ширину полосы канала связи). Уменьшение частоты приведет к уменьшению количества информации, передаваемой в единицу времени, т. е. пропускной способности линии связи. Таким образом, явление дисперсии ограничивает ширину полосы и пропускную способность оптической линии связи. Для передачи больших потоков информации с высокой скоростью следует использовать волоконные световоды, которые обладают как можно меньшей дисперсией.

В волоконных световодах имеют место 4 вида дисперсии:

- межмодовая;

- волноводная (внутримодовая);

- материальная;

- поляризационная.

Межмодовая дисперсия возникает в многомодовых волокнах и является для них основным видом дисперсии. В многомодовых световодах сигнал распространяется в виде совокупности большого числа мод, причем чем выше порядок моды, тем под большим углом к оси световода она распространяется. Время распространения моды от входного до выходного торца можно определить по формуле

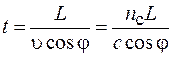, (84.1)

где 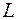– длина световода; 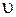и 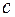– соответственно скорости света в сердцевине и вакууме. Для осевой моды 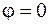, а для моды высшего порядка, которая может распространяться в световоде, 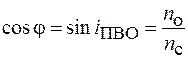. Тогда из (84.1) следует, что задержка распространения для этих мод, которая характеризует дисперсию, будет равна

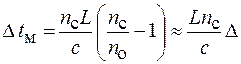. (84.2)

Из (84.2) видно, что дисперсия прямо пропорциональна длине световода и относительной разности показателей преломления 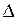. Величину дисперсии характеризуют задержкой 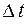, отнесенной к единице длины световода. При этом в качестве единицы длины берут 1 км, и тогда для межмодовой дисперсии в многомодовых волокнах имеем

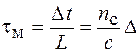. (84.3)

В градиентных многомодовых волокнах межмодовая дисперсия оказывается значительно меньше, чем в ступенчатых. Моды низших порядков распространяются вблизи оси световода, где показатель преломления больше, а скорость распространения меньше. Моды высших порядков проходят в световоде больший путь, но при этом заходят в область с меньшим показателем преломления, а это ведет к выравниванию времени распространения осевых и внеосевых мод. Межмодовую дисперсию градиентных волокон можно оценить по формуле

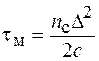, (84.4)

т. е. 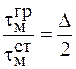. Так как относительная разность показателей преломления мала, то межмодовая дисперсия градиентных волокон в десятки раз меньше, чем ступенчатых. В ступенчатых волокнах при многомодовой передаче 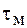~ 20…50 нс/км, в то время как у градиентных волокон 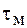~ 1…4 нс/км. В одномодовых световодах межмодовая дисперсия отсутствует, поэтому одномодовые кабели имеют значительно большую пропускную способность и это является их преимуществом.

Волноводная дисперсия обусловлена зависимостью скорости распространения каждой моды от частоты оптического сигнала. Этот вид дисперсии имеет чисто волновую природу и вытекает из решения уравнений Максвелла. Волноводная дисперсия наблюдается для всех волокон, однако в многомодовых она значительно меньше межмодовой и ею можно пренебречь. В одномодовых волокнах, наоборот, она становится одним из основных факторов, ограничивающих информационную емкость линии связи. Волноводная дисперсия зависит от монохроматичности излучения 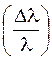. Использование лазера вместо светодиода в качестве источника оптического сигнала позволяет значительно снизить волноводную дисперсию.

Другим принципиально неустранимым видом дисперсии является материальная дисперсия. Она обусловлена зависимостью показателя преломления вещества световода от длины волны 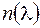. Вследствие этого даже для одной и той же моды излучение с разными длинами волн будет распространяться по волокну с разными скоростями.

С практической точки зрения важным обстоятельством является то, что для кварцевого волокна материальная дисперсия меняет знак вблизи длины волны 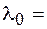1,27 мкм. При 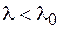она положительная, а для 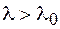становится отрицательной. В результате этого в области отрицательной материальной дисперсии происходит взаимная компенсация волноводной и материальной дисперсий, и для некоторой длины волны, называемой длиной волны нулевой дисперсии 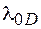, суммарная дисперсия равна нулю. Для кварцевых волокон с одной оболочкой 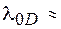1,31 мкм, что соответствует второму окну прозрачности. Если волокно имеет две оболочки, то за счет изменения волноводных параметров удается сдвинуть длину волны нулевой дисперсии в диапазон 1,5…1,6 мкм (третье окно прозрачности). При использовании еще большего числа оболочек удается обеспечить почти постоянную и близкую к нулю дисперсию в диапазоне длин волн от 1,3 мкм до 1,65 мкм. Такие волокна используются в широкополосных одномодовых линиях связи, обеспечивая передачу информации со скоростями в десятки гигабит в секунду.

Поляризационная дисперсия обусловлена наличием механических напряжений в волокне (например, при изгибах) или отклонением формы сердцевины от цилиндрической. При этом скорости распространения двух волн с взаимно-перпендикулярными плоскостями поляризации оказываются различными. По порядку величины поляризационная дисперсия значительно меньше всех других видов дисперсии и ее следует учитывать в одномодовых волокнах с компенсированной хроматической дисперсией при скорости передачи информации 10 Гбит/с.