Биноминальное распределение.
Если случайная величина x, которая принимает значения с вероятностью
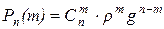
где m=0,1….n называется биноминальным.
Найти математическое ожидание, дисперсию такой величины x, можно рассматривать как наступление некоторого события а, при n – независимых испытаний в каждом из которых вероятность наступления одна и та же и равна р. Пусть хi – число наступлений событий а в i-том испытании.
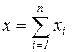
где xi имеет распределение
| xi | ||
| Р | q | p |
Тогда найдем математическое ожидание от x.
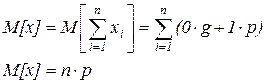
Из независимости испытания следует независимость xi. Дисперсия от суммы равна сумме дисперсий.
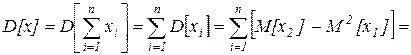
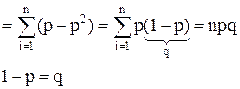
D[x]=npq
и среднеквадратичное отклонение
s[x]= 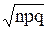
Пример: Вероятность отказа деталей за время испытания надежности равно 0,2. Найти М[x] и D[х], если испытанию больше подвергнуты 10 деталей.
n=10
p=0,2
M[x]=10×0,2=2 детали
1-р=q
1-0,2=0,8
D[x]×0,8×0,2=1,6; 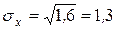
Дата добавления: 2015-08-14; просмотров: 716;
