Свойства дисперсии
1. Дисперсия постоянной равна 0.
Доказательство D[с]=0
D[с]=M[c2]-M2[c]=c2-c2=0
2. Постоянный множитель можно выносить за знак дисперсии, возводя ее в квадрат.
Доказательство:
D[cx]=c2D[x]
D[cx]-M[c2x2]-M2[cx]=c2M[x2]-c2M[x]=c2([M[x]2-M[x]])=c2D[x]
3. Дисперсия суммы независимых случайных величин
D[х+у]=D[х]+D[у]
D[х+у] = М[х+у]2-М2[х+у] = М[х2+2ху+у2]-(М[х]2+М[у]2)= М[х2]+М[2ху]+ М[у2]-М2[х]-М2[у] - М[2ху]= М[х2]-М2[х]+М[у2]-М2[у]=D[х]+ D[у].
Заметим, теорема обобщается на любое число взаимно независимых слагаемых. По определению следует, что дисперсия есть неотрицательное число и имеет квадратичную размерность.
Пример.
Найти дисперсию случайной величины , плотность распределения которой задана
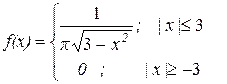 ;
;
 ;
;
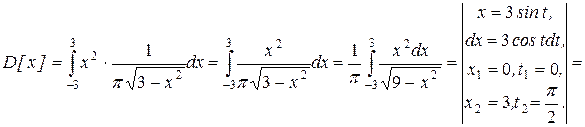
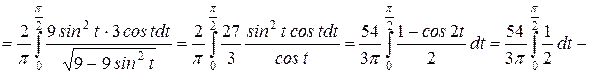
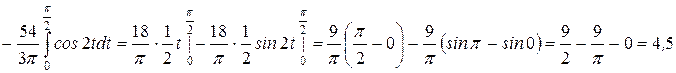
Пример № 2.
Число очков, выбиваемых при одном выстреле из 2-х стрелков, подчиняется следующему распределению:
| x1 | |||
| Р | 0,3 | 0,2 | 0,5 |
| x2 | |||
| Р | 0,1 | 0,6 | 0,3 |
Найти дисперсию случайных величин x1 и x2.
M[x1]=0,3+0,4+1,5=2,2;
M[x2]=0,1+1,2+0,9=2,2;
D[x1+x2]=D[x1]+D[x2]=M[x12]-M2[x1]+M[x22]-M2[x1];
| x12 | |||
| Р | 0,3 | 0,2 | 0,5 |
| x22 | |||
| Р | 0,1 | 0,6 | 0,3 |
M[x12]=0,3+0,8+4,5=5,6;
M[x22]=0,1+2,4+2,7=5,2;
D[x1+x2]=5,6-4,84+5,2-4,84=10,8-9,68=1,12.
D[x1]=0,76;
D[x2]=0,36.
Дата добавления: 2015-08-14; просмотров: 651;
