Функции управления в конвейерных системах.
Аппаратное управление инициациями.
Основная функция управления состоит в определении момента, когда может быть сделана новая инициация. Этот момент зависит как от свойств соответствующих таблиц занятости, так и от времени фактически поступления данных на вход конвейера. Имеется несколько типовых комбинаций, охватывающих весь диапазон от конвейера со статической конфигурацией и жесткой временной организацией до конвейера с динамической конфигурацией, при которой время поступления данных заранее не определено. Для статического конвейера из полученного цикла периода Р можно сформировать р- разрядный вектор i-ый разряд этого вектора равен нулю, если в i-ой единице времени любого цикла создается новая инициация . Затем простой контроллер со сдвиговым регистром может выбрать этот вектор и циклически сдвигать его на один разряд за один период синхронизации. Если в момент поступления синхроимпульса в самом левом разряде находиться 0, то в этот период начинается новая инициация.

Рисунок 12.27.
Гибкость управления, показанного на рисунке 12.27, состоит в его способность адаптироваться к новым расписаниям, подстраиваться к изменению векторной функции, либо ко времени поступления входных данных. Однако, для любых случаев желаемое расписание должно вычисляться заранее, система не обладает способностью к самодиспетчеризации.
Следующий по сложности и достаточно общий случай – это конвейер со статической конфигурацией, поступление данных в котором нельзя предсказать. Такое может быть, когда данные поступают из разделяемой памяти, а память время от времени оказывается занятой другими запросами, тогда как конвейеру требуются данные. В таких случаях невозможно определить точное, оптимальное расписание заранее так как невозможно определить момент поступления данных. Однако, гибкий контроллер, предложенный Дэвидсоном, может следовать жадной стратегии в реальном масштабе времени. В этом случае, разработчики конвейера могут так построить таблицу занятости, что все жадные циклы будут оптимальны или субоптимальны. В таком контроллере, по существу, реализованы правила генерирования диаграмм состояний, представляющий действия конвейера (рисунок 12.28).

Рисунок 12.28.
В начальный момент времени в сдвиговом регистре находится начальный вектор состояний, операции выполняются следующим образом:
· В начале любого периода синхронизации вектор сдвигается влево на 1 разряд.
· Если в левом разряде стоит 1, то инициация не может быть осуществлена в данный момент (период синхронизации).
· Если в левом разряде стоит 0 и имеются данные, то осуществляется инициация, а начальный вектор столкновений модифицируется операцией ИЛИ, применяемой к нему и вектору в сдвиговом регистре.
· Если в левом разряде стоит 0, но данных нет, то инициация не выполняется, а содержимое сдвигового регистра не модифицируются.
Если данные имеются в наличии всегда, то ясно, что содержимое сдвигового регистра всегда соответствует жадным циклам. Если же наступает жадная латентность, а данных в наличии нет, то это благоприятная возможность пропускается , что заставляет контролер отказаться от жадной стратегии. Однако, как только данные оказываются в наличии, выбирается следующая доступная латентность и после этого контроллер следует жадному циклу.
Этот контроллер гибкий: достаточно изменить начальный вектор столкновений, что бы изменилось поведение системы.
Если начальный вектор никогда не изменяется, то модификация этого контроллера может следовать стратегиям, отличным от жадной.
Здесь с выхода сдвигового регистра данные поступают в ПЗУ или ПЛМ в режиме поиска таблицы. Для любого возможного состояния конвейера у которого левый разряд равен нулю имеется запись в таблице, указывающая можно или нельзя осуществлять инициацию в этот момент времени. Выходные данные, как и ранее, комбинируются с сигналом «данные имеются» для определения того будет ли фактически производиться инициация. Записи в таблице выбраны так, чтобы всюду, где это возможно направлять конвейер, по оптимальному циклу. Как и ранее, у этой системы нет способа определения будущих моментов поступления данных, поэтому она может не вырабатывать оптимальных последовательностей инициаций.
Наиболее сложный случай возникает (рисунок 12.29), когда конфигурация конвейера изменяется динамически, а данные для каждого типа функций поступают независимо от остальных и непредсказуемо во времени (например, поток команд, поступающих на устройство декодирования команд).
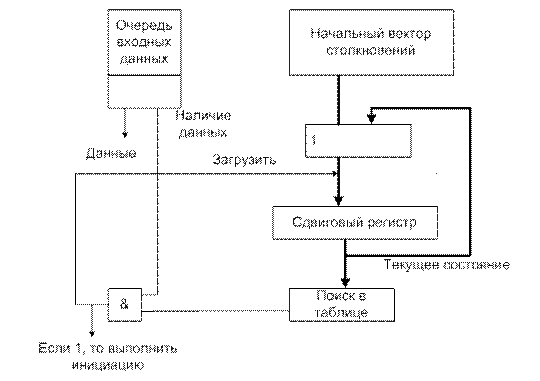
Рисунок 12.29.
В этом случае также невозможно динамически вычислить оптимальное расписание. Однако, как и ранее, можно реализовать контролер, который будет последовательно придерживаться жадной стратегии (рисунок 12.30).

Рисунок 12.30.
Имеется m начальных матриц столкновений и m сдвиговых регистров, представляющих текущее состояние матриц столкновений. Все регистры сдвигаются и загружаются одновременно. Выход i-го сдвигового регистра указывает на может или нет осуществляться инициация i-го типа в текущий момент времени. Эти выводы комбинируются с помощью операции логической И с соответствующими сигналами о наличии данных, поступающих из буферов входных данных. Комбинированные сигналы подаются затем на функциональный блок поиска в таблице (ПЗУ, ПЛМ). По этим входам в таблице выбирается наибольший совместимый набор инициаций, и данные всех выбранных типов одновременно вводятся в конвейер. Матрица столкновений затем обновляется с помощью операций логического ИЛИ над ней и над копиями соответствующих начальных матриц столкновений. Как и раннее, этот контроллер может быть расширен так, чтобы вырабатывались последовательности инициаций более общего вида, однако, в силу большого размера матрицы столкновений это расширение оказывается слишком дорогим для любого конвейера кроме тривиальных.
Внутриконвейерное управление.
После того, как инициация осуществлена, связанные с ней данные должны продвигаться в конвейере по пути, соответствующему таблице занятости и матрице столкновений. Механизм, который планировал инициацию и привел в действие, уже не связан с дальнейшими действиями. Однако во всех конвейерах требуется еще большой объем работы системы управления для проведения инициации и доведения её до конца. Работа системы управления включает в себя:
1. Генерирование сигнала инициация завершена.
2. Активизация логики внутри ступени.
3. Управление маршрутом.
4. Выбор функции внутри ступени.
Генерирование сигнала о завершении инициации связано с внешними устройствами, которым может требоваться информация о завершении функции.
Хотя это и не всегда необходимо, бывают случаи, когда логика внутри ступени должна иметь информацию о том, следует ли ей обработать данные во время того или иного цикла. Например, ступень конвейера сумматора с плавающей запятой, которая выполняет проверку на переполнение, не должно выставить флажок-индикатор ошибки до тех пор, пока не будет установлено, что образовались подлинные данные, а не просто совершается холостой цикл.
Управление маршрутом включает в себя фиксацию путей между ступенями необходимую для реализации таблиц занятости. Для некоторых простых конвейеров со статической конфигурацией такое управление не требуется. В случае сложных динамических конвейеров управление маршрутами может зависеть от типа выполняемой инициации и текущего шага использования. Это может потребовать индивидуального управления всеми входами.
Управляющие сигналы могут изменять функцию выполняемую ступенью. Существует много способов реализации всех режимов управления. Простая реализация первых двух-«инициация завершена» и «данные подлинные»-состоит в добавлении одного дополнительного разряда на фиксатор ступени, который управляется также, как и остальные разряды, но соединяются с соответствующим дополнительным разрядом следующей ступени с помощью холостой логики, которая просто повторяет его значение (рисунок 12.31).
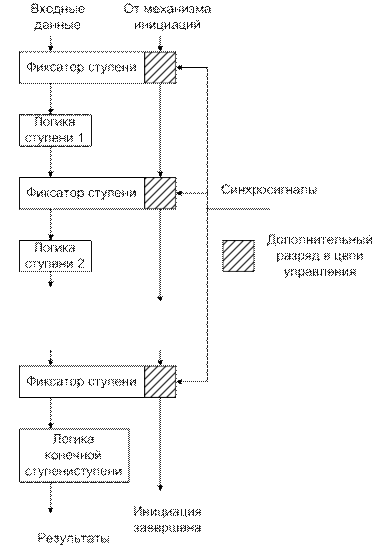
Рисунок 12.31.
Когда начинается новая инициация, в первый из этих дополнительных разрядов вводится единица. Для первой ступени это означает, что в настоящее время он имеет подлинные данные. При поступлении любых синхросигналов введенная единица переходит в следующую ступень и активизирует ее.
Наконец, на последней ступени эта единица в дополнительном разряде означает завершение операции. Заметим, когда две или более ступени активизируются одновременно (несколько меток в одном столбце таблицы занятости), все эти ступени будут получать единицу в свой дополнительный разряд. Точно также, когда с двух ступеней поступает два операнда на одну ступень, в её дополнительный разряд заносится единица лишь один раз. Наконец, такая реализация даёт некоторую возможность выявления ошибок, например, выявления попытки двух разных ступеней загрузить фиксатор одной ступени в одно и тоже время( столкновение).
Управление маршрутом и управление выбором режимов функционирования также тесно связаны между собой, и очень часто их аппаратная реализация схожа. В зависимости от механизма инициации, сложности таблицы занятости и степени реконфигурации эти механизмы могут быть либо управлением с привязкой ко времени либо управлением с привязкой к данным.
Механизм с привязкой ко времени обеспечивает управление маршрутом и сигналами выбора функции для всего конвейера. Исходя из наличия единого источника управления, внешнего по отношению к конвейеру привязанные по времени сигналы (рисунок 12.32) управление обеспечивает одновременно управление логикой одной ступени, маршрутом, ведущим в фиксатор другой ступени и адресами регистров файла третьей.
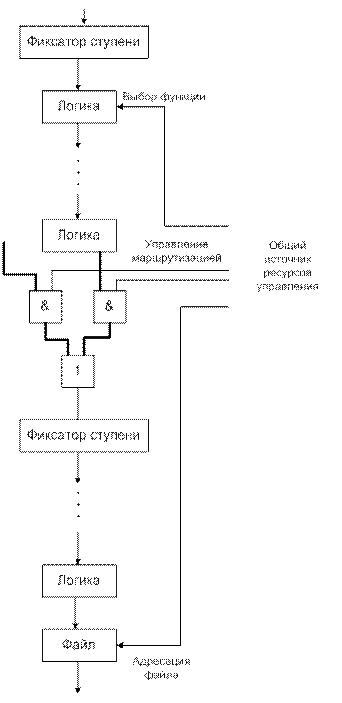
Рисунок 12.32.
Для конвейеров со статической конфигурацией это управление может быть либо жёстко фиксировано аппаратно, либо иногда изменяться, когда изменяется цикл или таблица занятости. Для более динамичного конвейера может происходить изменение общих управляющих сигналов с приходом каждого синхроимпульса.
Источники управления могут быть различными: от отдельного регистра до выхода блока микропрограммного управления. Основная особенность, однако, в том, что в любую единицу времени эти сигналы управляют состоянием машины в целом.
При управлении с привязкой к данным сигналы управления «сопровождают» данные по конвейеру, обеспечивая по мере необходимости управление на любой ступени. Централизованного источника управления нет. Вместо этого, всякий раз, когда осуществляется инициация, сигналы управления для соответствующих таблиц занятости поступают в конвейер наряду с данными. До тех пор, пока устройство инициации гарантирует, что столкновений не будет, нет опасности, что два управляющих сигнала попытаются одновременно использовать одну ступень. Один из возможных контроллеров с привязкой к данным, построенный по образцу временной цепочки, показан на рисунке 12.33.
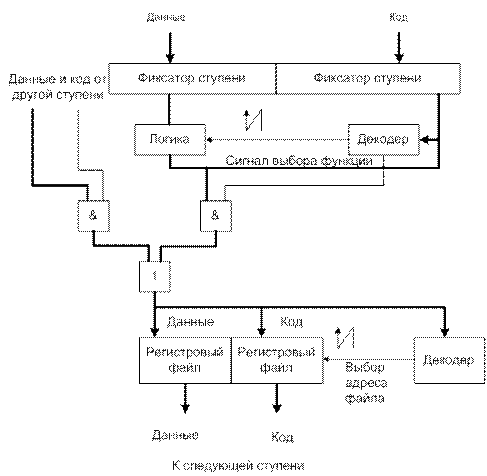
Рисунок 12.33.
Здесь дополнительный разряд активизации ступени заменен группой разрядов, содержащей некоторые код (вначале, например, номер таблицы занятости). Когда этот код поступает в какую-либо ступень, его можно декодировать для определения того, что должна делать логика. Например, какой путь должен быть выбран на следующем шаге и, быть может, в какую позицию регистрового файла поместить результаты. Вдобавок, некоторая логика может модифицировать этот код на основе результата данной ступени или на основе другой информации. Хотя такая организация более гибкая, чем привязка ко времени, но она является более дорогой.
Микропрограммное управление.
Микропрограммное управление должно вырабатывать в правильной последовательности различные сигналы управления, необходимые любой ступени. Подразумевается, что эти сигналы охватывают не только 4 режима внутриконвейерного управления, но и желаемую последовательность инициаций. Последнее достигается путем явного кодирования в структуре микропрограммы шагов, во время которых должны запускаться новые инициации. Недостаток здесь состоит в том, что последовательность инициаций должна вычисляться заранее с учетом того, что в дальнейшем во время исполнения ничего или почти ничего изменить невозможно. Однако, для широкого класса машин, к которым относятся многие векторные процессоры, это не является ограничением.
Концептуально, наиболее простым является такой блок микропрограммного управления, который при каждом синхроимпульсе подает на конвейер новую микрокоманду, которая интерпретируется как серия полей двоичных разрядов. Каждое поле связывается в точности с одной специфической операцией внутри конвейера, такой, как выбор функции для логики той или иной ступени. Во время исполнения этой операции содержимое поля интерпретируется для выборки управления данной функцией в течении данного периода синхронизации. Этот метод разбиения микрокоманд называется горизонтальным форматированием. Возможны и другие варианты, но горизонтальный форматирование является наиболее распространенным.
В качестве демонстрирации на рисунке 12.34 представлен пример двухступенчатого конвейера и центральная часть его микропрограммного контроллера.
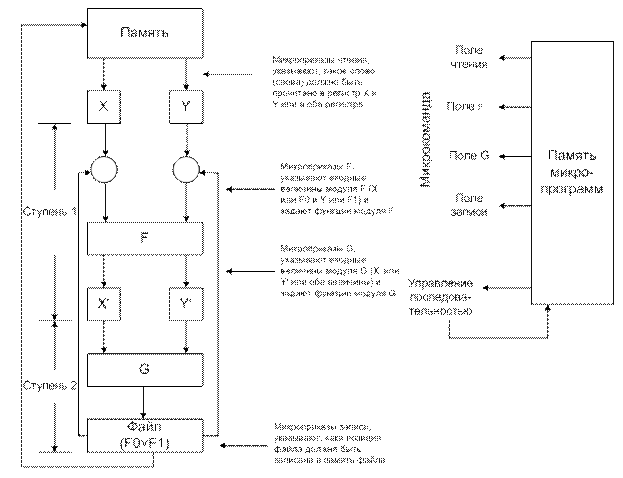
Рисунок 12.34.
Этот конвейер построен для сложения чисел с плавающей запятой, где логика первой ступени (модуль F) выполняет сравнение порядков и выравнивание мантисс логика двух ступеней (модуль G) выполняет сложение мантисс и нормализации результата. Данные берутся из памяти, проходят по конвейеру и возвращаются снова в память. Фиксатор на выходе модуля G является двухрегистровым файлом, любой из регистров которого в любой момент времени может быть загружен из G, его содержание может быть записано в память или возвращено на выход модуля
Каждая микрокоманда содержат 5 полей:
- поле чтения, указывающее, какие 2 слова надо прочитать из памяти в фиксатор X и Y;
- поле F указывающее, какие входы надо использовать( X, Y, Fo (позиция 0 регистрщвого файла) или F1(позиция 1 регистрового файла) и что должна делать логика модуля F (например, начать выравнивание входных величин, начать вычисление или передать данные с левого входа неизменными);
- поле G выбирает, что должен делать модуль G (сложить, вычислить или передать Х` неизменным), и куда поместить результат (в F0 или F1);
- поле записи выбирает, какую позицию регистра фала надо записать в память и куда именно;
- поле управления последовательностью указывает, как выбрать следующие микрокоманды из микропрограммной памяти. Оно должно содержать условные и безусловные переходы, причем одни из них могут базироваться на результатах самого конвейера или определяться счетчиком управления циклом. Во время каждого периода синхронизации “активно” в точности одно поле каждого типа.
Пример проектирования конвейера.
Пусть нужно спроектировать конвейер, который с периодическим интервалом принимает аналоговый сигнал Х, на любом интервале времени берет последние 4 значения Х(i), Х(i-1), Х(i-2), Х(i-3) и, применяя к ним симметричный фильтр, вычисляет выходную величину:
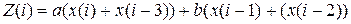
Считаем, что имеются следующие компоненты: одноступенчатые аналого-цифровые преобразователи (АЦП), двухступенчатый сумматор, одноступенчатый цифро-аналоговый преобразователь (ЦАП) (все с минимальным временем Т для ступени), четырехпозиционная память, способная выполнить одну операцию чтения или записи за Т секунд и двухступенчатый умножитель, способный принимать новые входные данные любые 2Т секунды. Наконец предполагаем, что имеется также любая логика необходимая для объединения всех компонент в систему.
Разбиение рассматриваемой функции на подфункции приводит к инициации, которая выглядит следующим образом:
1) использовать АЦП для получения Х(i);
2) циклически записывать это значение в четырехпозиционную память, так что в ней будут храниться Х(i),Х(i-1),Х(i-2),Х(i-3);
3) прочитать Х(i) и Х(i-3) и сложить их;
4) результат шага 2 умножить на a;
5) прочитать Х(i-1),Х(i-2) и сложить;
6) умножить результат шага 5 на b;
7) сложить результаты шагов 4 и 6;
8) вывести результат шага 7 через ЦАП;
На основе этого разбиения можно составить возможную таблицу занятости (таблица 1).
Таблица 1.
| 1. АЦП | ||||||||||||||
| 2. 4-х позиционная память | ||||||||||||||
| 3. Суммирование, 1ступень | ||||||||||||||
| 4. Суммирование, 2 стпень | ||||||||||||||
| 5.Умножение, 1ступень | ||||||||||||||
| 6.Умножение, 1ступени | ||||||||||||||
| 7. ЦАП |
Числа в клетках таблицы соответствуют шагу разбиения. Из таблицы получим множество запрещенных латентностей {0,1,2,3,4,5,7} и начальный вектор столкновений 11111101. Из таблицы занятости следует, что нижняя граница для MAL равна 5 (5 меток во второй строке), а из вектора столкновений следует, что имеется хотя бы один жадный цикл средней латентности 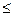 7 (7 единиц в векторе). Это показывает, что мы можем запускать новую инициацию в среднем, по меньшей мере, один раз на каждые 7 циклов, но не чаще, чем один раз на каждые 5 циклов. Что бы выяснить, что именно возможно, можно построить и проанализировать диаграмму состояний (отыскать вектор 11111101 в таблице). В результате находим, что (6) является оптимальным жадным циклом. При этом не достигается нижняя граница (5) для МАL и возможности ступеней оказываются недоиспользованными.
7 (7 единиц в векторе). Это показывает, что мы можем запускать новую инициацию в среднем, по меньшей мере, один раз на каждые 7 циклов, но не чаще, чем один раз на каждые 5 циклов. Что бы выяснить, что именно возможно, можно построить и проанализировать диаграмму состояний (отыскать вектор 11111101 в таблице). В результате находим, что (6) является оптимальным жадным циклом. При этом не достигается нижняя граница (5) для МАL и возможности ступеней оказываются недоиспользованными.
Теперь допустим, что разработчик системы хочет повысить её производительность, доведя среднюю латентность до 5, и хочет реализовать постоянный цикл латентности (5). Это возможно, что если все строки таблиц занятости могут быть выражены через максимальные классы совместимости отличительного множества Нс mod 5 цикла (5). Из леммы (приведенной выше) следует, что в эти классы входит набор {0,1,2,3,4} и все другие наборы, получаемые из него, прибавлением ко всем элементам константы и/или произвольных кратных числа 5.
С первой строкой таблицы занятости проблем не возникает; вторая строка имеет вид 1+{0,1,2,3,4}, так как удовлетворяет ограничениям. Точно также строки 5 и 6 имеют вид x+{0,1,2,3}, а строка 7 как 13+{0}. Проблема возникает со строками 3 и 4. Строку 3 можно представить как 4+{0,2,3+1х5}, что требует задержки операции 7 на один такт. Аналогичная ситуация наблюдается и со строкой 4. Всё это требует также задержки и операции вывода 8. Теперь таблица занятости имеет следующий вид (таблица 2):
Таблица 2.
| 1. АЦП | |||||||||||||||
| 2. 4-х позиционная память | |||||||||||||||
| 3. Суммирование, 1ступень | d | ||||||||||||||
| 4. Суммирование, 2 стпень | d | ||||||||||||||
| 5.Умножение, 1ступень | |||||||||||||||
| 6.Умножение, 1ступени | |||||||||||||||
| 7. ЦАП |
Таблица занятости с задержкой.
В качестве проверки устанавливаем, что начальный вектор столкновений имеет вид 111110101. Заглянув в таблицу начальных векторов, убеждаемся, что жадный цикл (5) теперь возможен и является оптимальным.
Одна из возможных аппаратных реализаций этой таблицы занятости показана на рисунке 12.35. Отметим, что некоторые фиксаторы ступени заменены на двухпозиционные регистровые файлы.
Некоторые из них, например файлы А и В используются потому, что задача требует двух отдельных сложений. Таким образом пара А0, В0 поддерживает сложение x(i)+x(i-3), пара А1,В1- x(i)+x(i-2). Точно также файлы Е и F поддерживают два умножителя. Предполагается, что частью инициализации является загрузка F0 и F1 двумя константами а и в. Наконец файлы С и D поддерживают заключительное сложение с его входной задержкой.

Рисунок 12.35.
Следующий шаг построения последовательностей латентностей (стратегия диспетчеризации) и конвейера заключается в том, что бы составить план работы конвейера во времени, которому должен следовать механизм управления. Так как период равен 5, а время вычисления равно 15, в любом наборе из 15 тактов будут иметься различные части 15/5=3 инициаций. Одна из инициаций только начинается, другая находится в середине вычислений, а третья заканчивается. При микропрограммном управлении важно, чтобы механизм управления отслеживал, в каком месте вычислений находятся все три инициации. Для формализации сказанного, разделим все время на наборы на 5 тактов в каждой инициации (таблица 3).
Таблица 3.
| i | i-1 | i-2 | |
| 5i | Преобразование аналог-цифра | Чтение x(i-1-2) в В1. Выдача маршрута для выходных данных сумматора к Е0 | Выдача маршрута для выходных данных к D0 |
| 5i+1 | Запоминание данных для преобразования в памяти | Запуск сложений А1 и В1 Запуск сложений Е0и F0 | |
| 5i+2 | Чтение x(i) в A0 | Выдача маршрута для выходных данных сумматора к Е1. Продолжение E0хF0 | Запуск сложений C0+В0 |
| 5i+3 | Чтение x(i-3) в В0 | Запуск умножения Е1хF1. Выдача маршрута для выхода данных умножения к С0 | Выдача маршрута для выходных данных сумматора к ЦАП |
| 5i+4 | Чтение x(i-1) в A1. Запуск сложения А0 и В0 | Продолжение умножения Е1хF1 | Выполнение преобразования цифра-аналог |
Предполагается, что в момент 5i i-я инициация только начинается, (i-1)-я находится на шаге 5 своих вычислений, а (i-2) начинает свой 10 шаг. В момент 5 i+1 все 3 инициации продвигаются на 1 шаг. Пустая клетка в третьем столбце означает задержку на один такт. Заметим, что запись в регистр D0 осуществляется момент 5i, а чтение из него в момент 5i+2, как и требуется для задержки на единицу времени. Однако, в данной задаче никакая другая инициация не делает попытки писать в файл D за этот период. Поэтому, строго говоря, нет необходимости использовать здесь регистровые файлы, достаточно иметь простой фиксатор. Однако, в общем случае подобный анализ необходимо вычислить, чтобы определить, необходимы или нет регистровые файлы.
После того как, такой анализ расписания проделан, можно использовать любую из методик управления описанную выше.
§12.9. Архитектура конвейерных систем.
Независимо от цели проектирования, большинство современных конвейерных векторов систем имеет общую архитектуру, показанную на рисунке 12.36.

Рисунок 12.36.
Основная память -единая память, содержащая как команды, так и данные в векторных и невекторных формах. Однако поскольку запросное отношение (число обращений на один синхроимпульс ) при использовании векторных команд оказывается гораздо более высоким, организация основной памяти существенно сложнее. Такая память, как правило, сильно расслоена.
Для всякой программы имеется (помимо векторных команд), необходимость в скалярных командах. К ним относятся тесты, операции зависящие от данных, операции ввода вывода, общее управление программой, управление памятью, функции операционной системы, а также определение векторов и настроек на них конвейера. Эти потребности лучше всего обеспечиваются традиционным набором команд. Поэтому в состав конвейерных векторных систем входит скалярный процессор.
Как только векторная команда выбрала вектор, контроллер берет все дальнейшее на себя. В функции этого устройства входит декодирование векторных команд, вычисление параметров адресации операндов, настройка генератора векторных адресов памяти и самого арифметического контроллера и отслеживание исполнения векторных команд. После завершения команды векторный контроллер выполняет все требуемые операции по очистке и выработке признака состояния.
Генератор векторных адресов памяти и контроллер, ответственный за преобразование параметров адресации, сгенерированных векторных контроллером на основе векторной команды, в серию запросов к основной памяти.
В силу различия между операциями векторного контроллера памяти, который за один такт обращается к относительно длинным сегментам векторов и самого арифметического конвейера, которому за один такт нужно иметь по одному операнду от каждого из нескольких входных векторов, большинство векторных процессоров содержит локальную память, которая работает, как буфер.
Арифметический конвейер –это аппаратное устройство, в котором, фактически выполняются арифметические действия, связанные с векторными командами. Конвейерное устройство может быть одно или несколько, при этом с изменяемой конфигурацией. Однако, во время использования отдельной векторной команды все устройства являются обычно устройствами со статической конфигурацией и выполняют повторные инициации желаемой таблицы занятости.
В заключении отметим, что эта типовая архитектура проявляет конвейерные свойства и способность к перекрытию не только на уровне арифметического конвейера. В то время, когда одна или несколько векторных команд используются векторными контроллерами, можно подготавливать следующую векторную команду, тогда как скалярный процессор может исполнять команды для обеспечения очередной векторной команды.
Структура команд.
Любая команда, скалярная или векторная, должна задать информацию, по меньшей мере, четырех общих типов:
· функцию, которая должна быть исполнена;
· операнды, которые должны быть использованы;
· статус, который должен быть зафиксирован;
· следующую команду, которая должна быть исполнена.
Задание функции (кода операции), эквивалентно выбору той таблицы занятости, которая должна использовать арифметический конвейер, когда данные будут в наличии.
Обычно это задание является двоично-кодированным индексом, значение которого используется векторным контроллером для выбора, как хранимой где-то таблицы занятости, так и соответствующей ей последовательности инициаций. Эти таблицы занятости и последовательности инициаций реализуются обычно либо аппаратно, либо микропрограммно и не могут непосредственно изменяться машинными командами. Хотя общее число типов операций векторного процессора может быть сравнительно небольшим, все же число векторных кодов операции в два или три раза превышает число сопоставимых с ним скалярных кодов. Причина в том, что если для скалярного процессора имеется только один способ выполнить сложение, а именно сложить данные имеющиеся на двух входах, то в случае сложения векторов допустимо несколько вариантов: поэлементная операция, редукционные команды, которые при сложении векторов вырабатывают единственный выходной скаляр и т.п.
Существенное различие между векторными и невекторными командами состоит в спецификации операндов. В невекторной команде операнд либо задаётся неявно (в аккумуляторе), либо может находиться в одном из доступных программисту регистров, либо является словом памяти, адрес которого вычисляется по базовому индексу или смещению.
Типичный формат команды - двухадресный. В векторной машине операнд может состоять из многих элементов, а его длину обычно нельзя предсказать. Вследствие этого почти все элементы векторного процессора хранят свои операнды в памяти. Это означает, что форматы большинства векторных команд трехадресные (два входа, один результат), причем каждое адресное поле задает отдельную область памяти. Неявная адресация встречается весьма редко. В типичной векторной команде имеется несколько адресных полей памяти и любое из них должно задать гораздо больше информации, чем в случае невекторных команд. В эту информацию входит: начало вектора в памяти, размерность вектора (например, одномерная решетка или двумерная матрица), число градаций по каждой размерности (размер), тип данных (целое число, плавающая запятая, полуслово или байт), расположение элементов в памяти. По целому ряду причин элементы векторов не всегда попадают в смежные слова памяти. В качестве примера можно привести обращение к столбцу матрицы, хранимой по строкам, т.е. важным является расположение элементов памяти.
Помимо выполнения заданной функции, типичная скалярная команда, такая как сложение, обнаруживает и фиксирует информацию о статусе (признак). Имеется, по меньшей мере, два рода такой информации. Первый относится к таким свойствам, как знак результата или равенство его нулю. Второй указывает на зависящие от данных ошибки (переполнения, деление на нуль и т.п.). Признаки запоминаются в специальных регистрах - регистре признаков. Затем команды перехода проверяют содержимое этих разрядов. Обнаружение состояний, к которым приводят ошибки, зависящие от данных, вызывает прерывание, приводящее к выходу из исполняемой программы на специальную подпрограмму, обрабатывающую прерывание.
Векторные команды должны оперировать с признаком такого же рода, но поскольку они имеют дело не с одноэлементным, а с многоэлементным результатом, для них используются другие методы. Например, было предложено, по меньшей мере, четыре способа оперирования с признаком таким как равенство результата нулю. Первый способ состоит в том, чтобы расширить состав информации в регистре, аналогичном регистру признаков, и помещать в него информацию о том, что ни один из результатов не равен нулю, или что некоторые результаты равны нулю, или что все они равны нулю. Второй способ заключается в регистрации числа нулей и места, где встречается первый из них. Третий способ состоит в формировании вектора кодов признаков, вследствие чего каждый элемент на выходе будет иметь не только значение, но и связанный с ним его собственный код признаков. Для этого требуется, что бы векторные команды содержали не только адресацию результатов, но и адресацию вектора признаков. Наконец, распространенный подход состоит в том, чтобы признаки вообще не запоминаются . Вместо этого, набор команд расширяется векторными командами типа: «сравнить векторы на равенство», «проверить на отрицательность». Каждая из этих команд принимает входные векторные операнды и вырабатывает на выходе другой вектор, имеющий ту же длину, что и входной, но такой, что каждый элемент в нем является отдельным разрядом фиксирующим результат проверок. Такие вектора называются двоичными векторами. Как только в архитектуру включаются двоичные вектора, становится потенциально полезным целый набор дополнительных команд. Сюда относятся полный набор векторных логических операций, которые производят поэлементные логические операции. Эти команды позволяют покаскадно осуществлять проверки. Например, найти все элементы вектора X, значения которых равны нулю или отрицательны, но не превышают соответствующих значений элементов вектора Y.
Обработка особых состояний в случае векторных команд также отличается от их обработки в случае скалярных команд, потому, что векторная команда выполняет более одной операции. В конвейерной машине в момент обнаружения одной ошибки может использоваться несколько инициаций соответствующих таблиц занятости и может оказаться неосуществимым «мягкий» останов процесса, после которого вычисления могли бы начаться с помощью подпрограммы, выполняющей исправления. Поэтому, управляющую информацию, задаваемую программистом, можно расширить так, чтобы она содержала разряды, предписывающие аппаратуре фиксировать события, но продолжать исполнение команды и накладывать на выходные данные «заплаты» некоторым стандартным способом. Типичный способ наложения «заплат» может состоять в замене результата нулём, если произошло переполнение в сторону младших разрядов, или замене его максимально большим числом, которое можно представить в разрядной сетке машины.
Даже простая фиксация особого состояния создает в векторном процессоре проблемы с организацией работы. Расширенный скалярный код признаков может показать, имеются ли ошибки, и быть может, где произошла одна из них, но он не покажет, сколько всего было ошибок и где произошли остальные. Вектор кодов признаков может показать, где именно произошли ошибки в многих векторных командах, но он бесполезен, когда каждый результат зависит от нескольких операций и от нескольких или даже всех входных данных (скалярное, матричное умножение). Поэтому большинство векторных архитектур в таких случаях либо прекращает выполнение команд, либо производят некоторые автоматические исправления и продолжают её исполнение, причем пользователю выдается, самое большее, расширенный код признаков.
Есть еще некоторые особенности в векторных конвейерных системах. К ним относятся заполнение и специальный формат данных - векторный с плавающей запятой.
Заполнение – это автоматическое удлинение вектора для уравнивания его длины с длиной некоторого другого вектора, который также служит входным для одной и той же команды. Здесь используются два метода: либо последний элемент повторяется столько раз, сколько нужно, либо производится заполнение нулями.
Использование специального формата данных – векторного с плавающей запятой - заключается в следующем. Стандартное представления числа с плавающей запятой содержит три компонента: знак, порядок и мантиссу. Однако, если известно, что элементы вектора примерно одинаковы, то можно достичь экономии памяти, если использовать единый порядок во всех элементах вектора. Как правило, этот общий порядок должен быть наибольшим из порядков, используемых любым элементом вектора. Можно использовать память, сэкономленную благодаря устранению индивидуального порядка для расширения мантисс. Это значительно повышает относительную точность представления чисел.
Способы адресации векторов.
Производительность векторных команд очень часто полностью определяет скоростью, с которой операнды могут извлекаться из основной памяти, а производительность арифметического конвейера оказывает на неё лишь второстепенное воздействие. Поэтому способы адресации имеют большое значение. Имеются два общих класса адресации векторов: плотный/регулярный и разряженный. Первый соответствует случаю, когда схемы расположения данных в памяти более или менее известны заранее. Второй – случаю, когда желаемая схема расположения данных должна вычисляться динамически.
Плотные/ регулярные схемы адресации. Обычный метод хранения векторов в памяти, при котором соседние элементы хранятся в ячейках, адреса которых достаточно близки и структурно упорядочены, называются плотным или регулярным. Имеются три разновидности таких схем: последовательные, непоследовательные но регулярные, подматричные. При последовательном способе соседние элементы вектора хранятся в соседних ячейках. Так, если элемент V(i) хранится в ячейке k, то V(i+1) в ячейке k+1 и так далее. Это можно распространить на двумерные матрицы одним из двух способов: размещение по строкам (строка занимает N последовательных ячеек, а сами строки также хранятся последовательно) или размещение по столбцам (аналогичное).
Следующий способ используется, когда нужен столбец матрицы, хранимой по строкам или нужна строка, хранимая по столбцам. В этом случае соседние элементы расположены не в последовательных ячейках, а по регулярной схеме: по одному элементу в каждом N слове (матрица RxN). Генератор векторных адресов должен сгенерировать серию адресов, значение которых отличается от N. Поскольку матрицы могут быть разные, значение N должно быть включено в команду.
При третьем способе требуется обращение, упорядоченное по строкам, к подматрице mxn матрицы RxN, хранимой по строкам. Здесь требуется m наборов по n последовательных адресов, причем начало любого набора на N единиц больше начала предыдущего. Это соответствует чтению n последовательных слов, пропуску следующих N-n ячеек и снова чтению. Этот способ требует включения в векторную команду двух параметров: n и N-n или некоторой их разновидности. Время доступа к вектору при любом из этих способов сильно зависит от структуры памяти (простое или сложное расслоение).
Разрешенные схемы адресации. Хотя схемы адресации, описанные выше, являютсясамыми распространенными, все же во многих приложениях они являются непригодными и неэффективными. К таким приложениям относятся: операции, зависящие от данных, обработка разреженных векторов, косвенный просмотр таблиц. В операциях, зависящих от данных, участие элемента вектора в операции зависит от его значения, у разреженных векторов большинство значений равно нулю. Хранение полного вектора в таких задачах требует огромных объемов памяти и сильно снижает потенциальную производительность, так как большинство операций тривиально (в них участвуют одни нули).
Все эти приложения требуют методов доступа, называемых разреженной адресацией. Двумя, наиболее распространенными средствами, обеспечивающими такую адресацию, являются двоичные векторы и векторы индексов.
Двоичный вектор имеет в качестве компонент 1 или 0.
Имеются три способа встраивания управления на основе двоичного вектора в векторные команды: селективное запоминание, сжатие, расширение.
При селективном запоминании векторная команда содержит для выходного вектора не только его адрес, но и двоичный вектор такой же длины. I-я компонента выходного вектора запоминается в том случае, если i-ый разряд двоичного вектора содержит единицу. Если в разряде находится нуль, то запоминание блокируется, и соответствующие значения в памяти остаются неизменными. Операции сжатия и расширения являются взаимно обратными. При сжатии (таблица 4) двоичный вектор имеет такую же длину, как и вектор данных. При этом используются только те компоненты вектора данных, для которых соответствующий разряд двоичного вектора равен единице. При этом сильно сокращается количество данных, подаваемых, например, на конвейер.
Операция расширения (таблица 5) расширяет вектор данных до размерности двоичного вектора.
| Таблица 4. | Таблица 5. | ||||||||||||
|
| ||||||||||||
| Сжатие данных. | Расширение данных. |
Однако реализация двоичных векторов имеет свои последствия. Структура генератора векторных адресов является более сложной, так как генератор должен получать доступ к двоичным векторам и использовать их для своих целей: просмотр и генерация адресов памяти. Кроме того, структура арифметического конвейера также должна быть расширена для генерирования двоичных векторов и для операций над ними (И, ИЛИ, сравнение). Необходим расширенный набор команд управляющих двоичными векторами.
Второй основной метод разреженного доступа – это использование векторов индексов разрежения, являющихся векторами, составленными из чисел, используемых либо непосредственно как адреса памяти, либо как смещения по отношению к некоторому указателю памяти.
Доступ к вектору при управлении с помощью индексов разрежения включает в себя чтение элементов вектора индексов разрежения и применения его для образования другого адреса памяти, указывающего фактические данные.
Здесь также возможно несколько основных вариантов, включая разреженное сдваивание и селективное чтение /запись.
При разреженном сдваивании вектор индексов указывает, какие элементы векторных данных не равны нулю. Не нулевые значения хранятся как отдельный вектор данных той же длины, что и у вектора индекса (таблица 6).
Таблица 6.
| Вектор индексов | Вектор данных | Эквивалентное представление |
| 3.1 4.7 3.14 | 3.1 4.7 3.14 . . . |
Разреженное сдваивание.
Селективное чтение/запись сходно со сжатием и расширением под управлением двоичных векторов (таблица 7). Каждый элемент вектора индексов указывает номер компоненты вектора данных.
Вектор индексов обеспечивает единственный и эффективный способ реализации просмотра таблиц.
Таблица 7.
| Вектор данных | Вектор индексов | После сжатия |
| 1.1 2.2 3.3 4.4 5.5 6.6 7.7 8.8 | 1.1 4.4 5.5 8.8 |
Сжатие с помощью векторных индексов.
Полная реализация векторов индексов (таблица 8) еще более сложна, чем реализация двоичного вектора, так как генератор векторных адресов должен выполнять два доступа памяти на одно слово данных: один доступ для вектора индексов, второй для данных. Кроме того генератор векторных адресов должен также складывать базы, сравнивать наборы индексов и объединять их. Таким образом, генератор векторных адресов сам становится подобным целому векторному процессору.
Таблица 8.
| Вектор данных | Векторных индексов | После расширения |
| 1.1 4.4 5.5 8.8 | 1.1 0* 0* 4.4 5.5 0* 0* 8.8 |
Расширение с помощью векторных индексов.
* - в зависимости от реализации эти значения могут быть и старыми.
Дата добавления: 2015-08-14; просмотров: 1137;
