Конвейеры с динамической конфигурацией.
В конвейерах с динамической конфигурацией любая инициация может относиться к своей таблице занятости, что оказывает глубокое влияние на диспетчеризацию. Во-первых, могут быть моменты времени, когда в течение одного периода синхронизации возможно одновременное осуществление более одной инициации. Во- вторых, здесь уже нет единственного определения оптимальной диспетчеризации. В статическом конвейере все инициации одного типа, поэтому та стратегия, которая максимизирует темп обработки этих инициаций, является ,очевидно, оптимальной. Если же использовать много таблиц занятости, то может быть несколько в равной мере обоснованных оптимальных стратегий, включая максимум общего числа инициаций любого типа, максимум общего числа инициаций при условии, что в общем числе инициаций определенный процент должны занимать таблицы занятости любого типа; минимизации общего времени, требуемого для обработки специфических последовательностей инициаций для таблиц занятости разных типов.
Модифицированные диаграммы состояний.
Диаграмма состояний для статического случая обобщается на динамический случай.
Для каждого такта матрица столкновений указывает множество возможных инициаций. Матрица столкновений С- это двоичная матрица размерности rxd, где r-число таблиц занятости , а d- максимальное время вычисления для всех таблиц. Аналогично вектору столкновений элемент (j,k) матрицы равен нулю только в том случае, если новая инициация производится через k единиц времени после данного момента и относящегося к таблице занятости типа j не вызывает столкновений ни с одной из текущих инициаций.
Отличие этих диаграмм от статических диаграмм состоит в том, что теперь нет единственного начального состояния. Напротив, для r таблиц замен имеется r начатых состояний, из которых i-ое означает, что первая инициация в момент 0 была типа i. Матрица столкновений для этих состояний называется начальной матрицей состояний. Как и в статическом случае, эти матрицы представляет столкновения возникающие при одной инициации, следующей в точности одной за другой; j-я строка i-ой матрицы CМi является вектором столкновений между инициациями типа i и более поздней инициацией типа j.
Таким образом, элемент CМi(j,k) равен 0, если только сдвиг на к единиц вправо j-й таблицы занятости и ее наложение на копию i-й таблицы занятости не приводит к столкновению. Пусть заданы две таблицы занятости (т.з.)типов А и В (рисунок 12.25). 

| А | А | ||||||
| А | А | А | |||||
| А | А | А |
Таблица занятости типа А:
Запрещенные латентности для т.з. А-{0,2,4,6}
Вектор столкновений для т.з. А-(10101010)
| В | В | В | ||||||
| В | В | |||||||
| В | В |
Таблица занятости для В
Запрещенные латентности для т.з. В-{0,1,2,5,6,7}
Вектор столкновений для т.з. В-(11100111)
Рисунок 12.25.
Общая таблица занятости для т.з. А и В
| В | В | А | А | В | В | |||
| А | В | А | В | А | ||||
| А | А | В | В | А |
Запрещенные латентности при сдвиге т.з. В относительно т.з. А
{1,2,3,4};
Вектор столкновений при сдвиге т.з. В относительно т.з. А
(01111000)
Запрещенные латентности при сдвиге т.з. А относительно т.з. В
{1,2,3,4,5}
Вектор столкновений при сдвиге т.з. А относительно т.з. В
(011111000)
Тогда начальные матрицы столкновений равны: занятости
Матрица 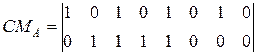
Матрица 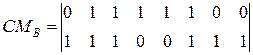
Во всех случаях i-я стока матрицы CMi совпадает с начальным вектором столкновений, который возник бы, если бы i-я таблица занятости применялась в статической конфигурации. Остальные строки CMi является кросс - векторами столкновений. Например, матрицы столкновений для конвейера, использующего только таблицы занятости А и В имеет вид:
Матрица 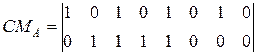
Матрица 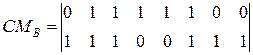
Фактическое построение основной части диаграммы сходно с построением для статического случая. Для любого состояния и любого столбца в матрицы столкновений этого состояния, содержащего хотя бы один 0, имеется набор других ведущих к новым состояниям.
Генерирование нового состояния состоит из сдвига старой матрицы столкновений влево и применяется логическая операция ИЛИ с соответствующими матрицами столкновений. Этот процесс усложняется, когда столбец содержит более одного нуля. Здесь возможны некоторые различные типы инициаций, и должна строиться отдельная дуга для каждой из возможных комбинаций, называемой набором инициаций. Например, если в некоторой матрицы столкновений в столбце k стоят нули в строках 1,3и 4, то может быть 7 различных дуг латентности k , а именно, дуги, связанные с набором инициаций {1},{3},{4},{1,3},{1,4},{3,4},{1,3,4}. Далее 0, стоящий в столбце, означает, что нет опасности столкновений ни с одной из ранее запущенных инициаций; он ничего не говорит о столкновениях с какой либо другой инициацией в том же наборе инициаций. Следовательно, не все наборы инициаций являются правильными. Чтобы набор инициаций обладал своей дугой, не должно быть столкновений между инициациями этого набора при их одновременном запуске. Это эквивалентно утверждению, что при комбинированном наложении таблиц занятости из данного множества совпадения меток не будет. Такое множество называется совместимым набором инициаций. Таким образом, из состояния, k-й столбец которого содержит несколько нулей, будет выходить по одной дуге для любого совместимого набора инициаций. Такие наборы содержатся среди подмножеств множества строк, имеющих нули в этом столбце. Каждая дуга, как правило, ведет к отдельному состоянию. Чтобы проследить, какая из инициаций вызывает тот или иной переход, каждая дуга имеет метку, содержащую не только ее латентность, но и соответствующий совместимый набор инициаций. Простой способ построения всех совместимых наборов инициаций, состоит в том, что сначала рассматриваются только максимально совместимые наборы инициаций. Поднабор C любого набора инициаций S является максимальным совместимым по отношению к S, если С совместим и добавлен к С любой таблицы занятости, находящейся в S, но не в С делает итоговый набор несовместимым.
Для любого S может быть несколько (возможно пересекаемых) максимальных совместимых поднаборов. Как только все такие максимальные совместимые наборы известны, можно утверждать, что совокупность всех совместимых наборов из S состоит из всех поднаборов всех максимальных совместимых наборов.
Лемма. Набор инициаций S совместим, если только для всех i и j из S выполняется CMi(j,0)=0.
Процедура построения этих максимальных совместимых наборов затем может быть скорректирована на основе процедуры описанной ранее.
Объединение всех предыдущих построений дает следующую процедуру создания модифицированных диаграмм состояний для конвейеров с динамической конфигурацией.
Процедура: Динамическая модифицированная диаграмма состояний.
1. Включить в начальное состояние любое состояние, соответствующее начальным матрицам столкновений.
2. Для любого еще не обработанного состояния, и для k-ого столбца матрицы столкновений этого состояния, в котором имеется хотя бы один ноль, построить все совместимые наборы инициаций.
3. Для любого набора инициаций выполнить операцию логического ИЛИ над совокупностью соответствующих ему начальных матриц.
4. Удалить первые k столбцов из матрицы столкновений текущего состояния, добавить к ней нули справа и выполнить операцию логическую ИЛИ с результатом шага 3. Назвать это новым состоянием и соединить с текущим состоянием дугой, имеющей метку в виде k и набора инициаций.
5. Построить все наборы инициаций, считая, что столбец состоит из одних нулей. Затем для любого состояния диаграммы и любого набора инициаций построить соответствующее состояние - адресат и дугу, указав значение >= d (d-время вычисления) и перечень элементов набора.
Часть диаграммы состояний для таблиц занятости А и В показана на рисунке 12.26.
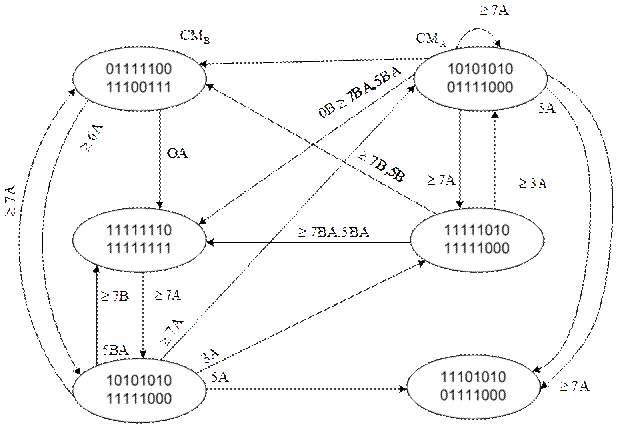
Рисунок 12.26.
В динамическом случае, в зависимости от системы возможен один из критериев производительности. Разумеется, для любого критерия требуется определенный метод анализа. Имеется, по меньшей мере , три различные меры производительности, в применении, к реальным конвейерам, а именно, определение максимального числа инициаций:
1) Любого рода и в любом порядке , приходящихся на единицу времени.
2) В единицу времени при условии, что часть инициаций должна приходиться на каждую таблицу занятости и что нет никакой упорядоченности для последовательности.
3) В единицу времени, если задана некоторая специфическая последовательность инициаций, которая должна выполнятся.
С переходом от пункта 1 к пункту 3 меры становятся все белее ограничительными. Первая является мерой максимально возможной производительности конвейера при любом режиме работы, и определяет верхнюю границу для двух других. Вторая – полезна, если известно, что имеется некоторая статистическая смесь типов инициаций ( например, 50% типа А, 20% типа В, 30% типа С), но недостаточно сведений о взаимосвязи очередной инициации с последующими. Третья является мерой производительности в том случае, когда должна выполняться специфическая последовательность событий.
В зависимости от целей разработчика и имеющеюся у него объема информации, может быть использована одна из трех указанных мер производительности. Измерения производительности первого рода выполняется легко, поскольку они сходны с анализом, применяемым к статическим диаграммам. Основное отличие состоит в том, что при вычислении средней латентности цикла его период делится не на число элементов цикла, а на общее число членов всех наборов инициаций, соответствующих дугам, образующим цикл. Так учитываются все выполненные инициации, даже если две из них запускаются одновременно. Например, цикл (5АВ,7В) имеет среднюю латентность 4, а не 6. Поскольку на один период синхронизации может приходиться больше одной инициации, то средняя латентность может быть меньше единицы. Такая ситуация невозможна в статическом случае. Так как в любой момент времени может быть инициализировано больше одной таблицы занятости, не существует способа определения по самим только таблицам занятости точной нижней границе средней латентности. Это еще одно отличие от статического случая, в котором латентность ограничивается числом меток в строке. Единственная граница определяется следующей леммой.
Лемма. Средняя латентность любого цикла (для конвейера с динамической конфигурацией) ограничивается снизу числом 1/n, где n - максимальное число элементов в любом наборе инициаций.
Доказательство следует из определения набора инициаций.
Вторая мера производительности определяет минимальную среднюю латентность при условии, что любая таблица занятости, инициируется в смеси в определенной доле случаев. Цель оптимального алгоритма диспетчеризации здесь состоит в отыскании цикла с минимальной средней латентностью, инициации которого относятся к данной смеси. Эту проблему можно попытаться решить с использованием некоторых результатов, полученных для статического случая.
Рассматриваются простые циклы. Каждый такой цикл имеет собственную смесь типов инициаций. Например простой цикл (3А,5А,5АВ,7А,7А) имеет смесь из 1/6 типов инициаций для таблицы В и 5/6-для таблицы А. Рассматриваются те простые циклы, которые имеют минимальную среднюю латентность для заданной смеси. Они называются хорошими простыми циклами. Если задан произвольный набор хороших простых циклов, то можно реализовать любую смесь ( в определенных пределах) как некоторую комбинацию составляющих циклов. Эти инициации могут содержать по несколько копий некоторых циклов. Например для цикла (1А,7А,3А,5А,0В,7А) и (3В,8В) повторение одного цикла дважды, а второго три раза приводит к смеси содержащей 44,44% типов инициаций для таблицы В.
При дальнейшей разработке этой идеи можно прийти к довольно сложному алгоритму ветвей и границ линейного программирования, который для каждой смеси обеспечивает вычисление той совокупности хороших простых циклов, которые попадает в эту смесь и достигает в ней минимальной средней латентности. Единственный недостаток этого алгоритма состоит в том, что он не гарантирует связности получаемой совокупности циклов. То есть может оказаться невозможным образовать единственный замкнутый путь в диаграмме состояний, который проходит по всем желательным циклам. Поэтому может потребоваться соединение циклов путями, которые не оптимальны, что приводит к снижению производительности.
Для третьей меры производительности используется некоторая последовательность типов инициаций, которым надо следовать. Здесь нет пока каких-либо разработанных методов диспетчеризации, за исключением исчерпывающего перебора.
По-видимому, лучшее, что можно сделать при таких обстоятельствах, это исследовать простые варианты жадной стратегии, которая среди дуг с подходящими набором инициаций выбирает дугу с минимальной латентностью.
Дата добавления: 2015-08-14; просмотров: 1400;
