Генерирование таблиц занятости на основе циклов.
Ранее, был рассмотрен случай, когда на основе таблицы занятости выработалась оптимальные циклы инициаций. Здесь рассмотрим обратную задачу: как, отправляясь от цикла определить свойства таблицы занятости, которая поддерживает этот цикл. Такой анализ возможно применить по меньшей мере к двум задачам. Во- первых, к задаче начального определения конвейеров, когда на разбиение на ступени еще не произведено, а функция которая должна им вычисляться и общие скорости решения уже известны. Во-вторых, к задаче, имеющей дело с данной таблицы занятости, MAL который не достигает нижней границы, когда исследование нескольких модифицированных таблиц занятости, может дать улучшенный результат.
Определим множество Gс интервалов инициации данного цикла С как множество всех целых чисел i, таких, что интервал между некоторой парой инициаций (не обязательно последовательных) равен i. Если цикл латентностей С есть (L(1), L(2), .. , L(k)), тогда < L(1), .. , L(k), L(1), .. , L(k), L(1), .. > эквивалентные последовательности латентностей, а Т(0),Т(1), Т(2), … - последовательность моментов инициации.
Здесь T(j)- начальный момент j-й инициации равен сумме латентностей предыдущих инициаций, то есть:
T(j)= 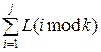
Тогда множество Gс записывается как
Gс = {T(i)-T(j), i>j }, где T(i) и T(j) принадлежат последовательности моментов инициации. Таким образом, Gс- множество интервалов между инициациями, когда инициации выполняются согласно циклу С. Для цикла (3,5,7) последовательностью латентностей будет <3,5,7,3,5,7,3,5,7, ..>, последовательностью моментов инициации- [0,3,8,15,18,23,30,33,38,45, …], а множеством Gс – множество {3,5,7,8,10,12,15,18,20,22,23,25,…}. Например, число 22 принадлежит к множеству Gс, так как инициации наступают в момент времени 30 и 8.
Если число i принадлежит множеству Gс ,то никакая таблица занятости, поддерживающая цикл С, не может иметь в одной строке двух меток, разделенных i тактами. В противном случае, i было бы запрещенной латентностью и не могло бы принадлежать к множеству Gс.
Удобнее рассмотреть дополнительное множество Нс = Z/Gс, где Z – множество всех целых неотрицательных чисел. Если i принадлежит к множеству Нс, то допустимо (хотя и не обязательно) разделять две метки в строке i тактами. Аналогично, допустимо иметь как 0 так и 1 в i-ом разряде начального вектора столкновений. Запишем строку таблицы занятости как множество {Z(1),Z(2), ..}, если метки стоят в ней в момент Z(i).
Пусть дан цикл С. Любая строка в любой таблицы занятости, которая поддерживает этот цикл должна быть представлена как {Z(1),Z(2), ..}, в которой для любых i,j |Z(i)-Z(j)| 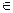 Hc (*)
Hc (*)
Если F – множество запрещенных латентностей таблицы занятости, то цикл с будет справедливой для нее последовательностью инициации, только если F является подмножеством Hc , что равносильно F 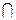 Gс =
Gс = 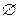 .
.
Доказательство очевидно и вытекает из предыдущих лемм. Так как множество Hc и Gс бесконечны, то их трудно использовать на практике. Заменим Hc и Gс на конечные множества.
Для любого i 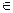 Gс
Gс
Gс mod P = {i mod P}/{0},
Hc mod P = Zp - Gс mod P ,
где Р- период цикла (то есть сумма латентностей), а
Zp = {0,1, … , Р-1}
Множество Gс mod P – это множество латентностей между инициациями, разделенными самое большее Р тактами, которое повторяется с периодом Р.
Для цикла (3,5,7) период Р=15, множество Gс mod P = {3,5,7,8,10,12},
а Hc mod P ={0,1,2,4,6,9,11,13,14}.
Часто оказываются полезными следующие свойства этих множеств:
1. Если g 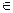 Gс mod P , то для любого i ≥ 0 (g+ip )
Gс mod P , то для любого i ≥ 0 (g+ip ) 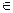 Gс
Gс
2. Если g 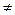 0 , то g
0 , то g 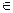 Gс mod P , только если (р-g)
Gс mod P , только если (р-g) 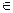 Gс mod P
Gс mod P
3. Если h 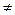 0, то h
0, то h 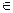 Hc mod P , если (р-h)
Hc mod P , если (р-h) 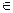 Hc mod P.
Hc mod P.
Теперь можно определить набор правил для построения таблицы занятости.
Пусть Zp = {0,1, … , p-1}. Два числа i,j из Zp совместимы по отношению к Hc mod P , если |i-j| mod P 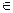 Hc mod P.
Hc mod P.
Классом совместимости относительно Hc mod P называется любое подмножество Zp , все пары элементов которые совместимы.
Максимальный класс совместимости относительно Hc mod P – это класс, который не является подмножеством никакого другого класса совместимости.
Например, для цикла (3,5,7) числа 9 и 13 совместимы, так как |13-9| mod 15 = 4 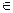 Hc mod P. Множество {0.9.13} является классом совместимости, тогда как множества {0,9,11,13},{5,6,7} и {0,1,2} является максимальными классами совместимости.
Hc mod P. Множество {0.9.13} является классом совместимости, тогда как множества {0,9,11,13},{5,6,7} и {0,1,2} является максимальными классами совместимости.
Если некоторое множество целых чисел {Z(1),Z(2), …} совместимо, то оно автоматически удовлетворяют условиям (*) и может служить строкой некоторой таблицы занятости, поддерживающей этот цикл. Верно и обратное : множество индексов любой строки таблицы занятости, поддерживающей данный цикл, должно быть совместимым. Таким образом, приходим к следующему :
Теорема: Для любого цикла С с периодом Р любая таблица занятости, поддерживающая этот цикл как последовательность инициаций, должна иметь строки вида:
{Z(1)+ i(1)P, Z(2)+ i(2)P, … }, где {Z(1), Z(2), … }- некоторый класс совместимости Hc mod P , а i(1),i(2), .. – произвольные числа.
Доказательство следует из предыдущих лемм.
Эта теорема позволяет построить целый набор таблиц занятости, поддерживающих некоторые циклы. Вычисляются все максимальные классы совместимости, и для любого подмножества некоторого класса используется предыдущая теорема для построения всех возможных строк.
Максимальные классы совместимости определяются с помощью перечислительных алгоритмов, так как отношение совместимости не транзитивно.
Рассмотрим пример, в котором при обнаружении несовместимости, множество расщепляется на два новых, ни одно из которых не содержит этой несовместимости. Хотя все множества, отыскиваемые алгоритмом, совместимы, некоторые из них являются подмножествами других и должны быть обращены. Алгоритм вычисляет только те максимальные совместимые множества, которые содержат Z(1) (в типичном случае 0).
Расширение предыдущих лемм показывает, что если некоторое подмножество S является совместимым множеством, то таким же будет и подмножество S' = { (S+a) mod P}; 1≤ a ≤ P-1, S 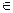 S'.
S'.
Следовательно, после завершения базового алгоритма остальная часть максимально совместимых подмножеств вычисляется простым сложением.
Исходное множество – все числа меньше Р. Определяем совместимость этого множества и 0 (всегда принадлежит множеству Hc) то есть |Z/{0}| относительно Hc mod P. Получаем само множество Hc mod P. Далее определяем совместимые множества в Hc mod P по следующей процедуре.
Процедура : определить множества (S,j).
(вычисляет все совместимые множества S; j – элемент в S)
1. Если j ≥ P, то добавить S к множеству всех совместимых подмножеств и выйти из процедуры.
2. Если j  S, то j:= j+1 и идти к пункту 1.
S, то j:= j+1 и идти к пункту 1.
3. Если j совместимо со всеми остальными элементами S, то j:= j+1 и идти к пункту 1.
4. Если U – множество всех элементов S, несовместимых с j, то:
| Определить множества (S-{j},j+1) | 
| Comment: |
| вернуться к началу процедуры | ||
| Определить множества (S-U,j+1) |
5. Удалить из множества совместимых подмножеств те, которые являются подмножествами других.
6. Для любого множества и для любого числа i в области 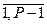 построить новое множество, любой элемент, которого является суммой по модулю Р числа i и элементов в исходном множестве.
построить новое множество, любой элемент, которого является суммой по модулю Р числа i и элементов в исходном множестве.
Например, для цикла (3,5,7) процедура имеет вид, показанный на рисунке 12.20:
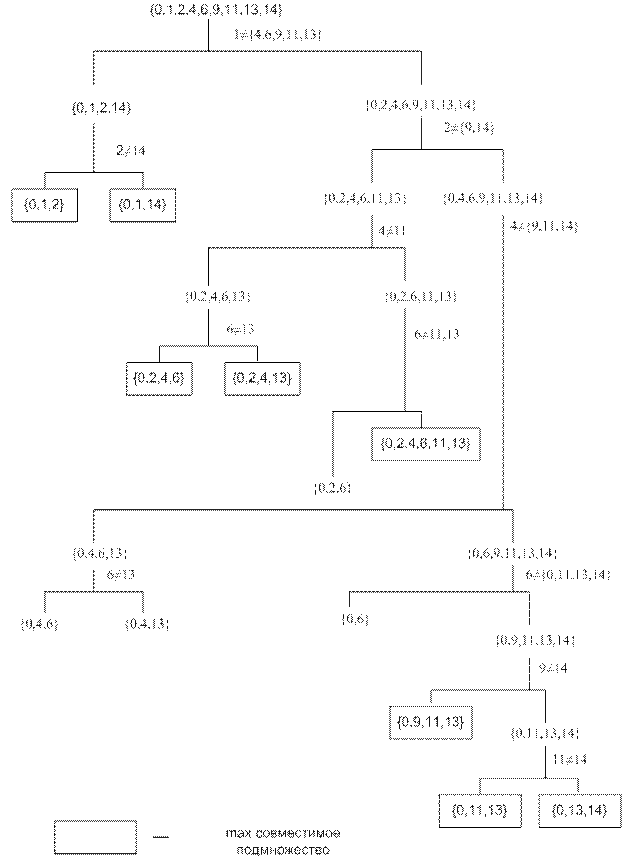
Рисунок 12.20.
Для получения всех максимальных совместимых подмножеств надо к полученным максимально совместимым подмножествам прибавить по mod P некоторое число i из 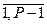 .
.
Например, из {0,2,4,13} образуется {1,3,5,14}, {2,4,6,0}, {3,5,7,1}, … Немаксимальные подмножества не учитываются.
Количество таблиц занятости, которое можно получить из этих максимальных множеств весьма велико. Ничто в вышеприведенной теореме не ограничивает числа ступеней и классов, используемых для построения той или иной ступени. Например, несколько вариантов таблиц занятости для цикла (3,5,7) следующие (рисунок 12.21):
| 
|
|
| Время Ступень | |||||||||||
| х | х | х | х | ||||||||
| х | х | х | |||||||||
| х | х | х | |||||||||
| х | х |
|
| Время Ступень | |||||||
| х | х | ||||||
| х | х | х | |||||
| х | х | х |
|
Рисунок 12.21.
Здесь одни строки являются максимально совместимыми множествами, а другие – подмножествами этих множеств. Некоторые строки имеют постоянное смещение.
Совершенные циклы.
Предыдущие результаты позволяют получать таблицы занятости, поддерживающие произвольные циклы латентностей. Какой же цикл лучше? Исходным параметром является средняя латентность. Однако, сравнение латентностей справедливо, если сами эти циклы определяются одной и той же таблицей занятости, определяемой одним и тем же конвейером.
Одним из существенных свойств цикла является степень использования им аппаратных средств, то есть показатель использования ступени (число меток умноженное на темп инициаций). Желательно иметь 100 % использование ступеней. Может быть другой цикл с большей латентностью, в которой обеспечивается 100 % использование хотя бы одной ступени. Можно указать верхнюю границу показателя использования любой ступени конвейера (таблицы занятости), поддерживаемого тот или иной цикл.
Циклы, для которых верхняя граница равна 100 % называется совершенными. Показатель использования ступени – это отношении числа меток в соответствующей строке таблицы занятости к средней латентности цикла. Но, в соответствии с вышеприведенной теоремой, любая строка в таблице занятости, поддерживающей тот или иной цикл должна относиться к классу совместимости по отношению к Hc mod P. Отсюда получим:
Теорема.Для любого цикла С максимальное возможное использование любой ступени (таблицы занятости), поддерживаемого этот цикл не превышает m/L.
m- число элементов в наибольшем классе совместимости по отношению к Hc mod P, L- средняя латентность цикла.
Это следует из того, что в соответствии с ранее приведенной теоремой, число меток в любой строке равно числу элементов класса совместимости. Взяв класс совместимости с наибольшим числом элементов, получим эту границу.
Для любого цикла существуют конвейеры (таблицы занятости), которые достигают этой границы для одной и более ступеней. Эта граница может быть достигнута путем использования при построении любой строки и всех строк максимального класса совместимости с наибольшим числом элементов.
Цикл является совершенным, только если m=L. Например, цикл (3,5,7) со средней латентностью равной 5 имеет самое большее 4 элемента в любом классе совместимости и, следовательно, максимальное использование им ступеней составляется 80 %. То есть он не совершенен, а вот циклы (5,3) и (1,7), которые также поддерживаются этой таблицей занятости (таблица А) совершенны, так как средняя латентность их равна 4.
Лемма. Если цикл постоянный, то есть имеет вид (L), то он совершенен. Для такого цикла Hc mod P является множеством {0,1,2, .. , L-1}, а множество {0,1,2, .. , L-1} совместимо. Оно имеет L элементов и таким образом граница использования L/L =1.
Начинать разработку таблицу занятости следует с рассмотрения совершенных циклов желаемой латентности. Если какая- то строка окончательной таблицы занятости построена на основе наибольшего класса совместимости, то исходный цикл автоматически оказывается оптимальным и никакой дальнейшей анализ не требуется.
Введение задержек для увеличения производительности.
Наиболее распространенная проблема, связанная с конвейером возникает, когда от уже существующего набора конвейерных аппаратных средств требуют использования нового типа вычислений. В подобных случаях разработчики почти не могут влиять на новую таблицу занятости, а анализ состояний при этом показывает, что наилучшая из возможных последовательностей инициаций не достигает нижней границы, то есть аппаратные средства остаются недоиспользованными. Было бы очевидно, полезным, если бы удалось модифицировать таблицу занятости так, что бы общая структура не изменилась, а общая производительность возросла. Такой способ существует и позволяет снизить среднюю латентность до нижней границы, увеличив время на одно вычисление. Это создается введением задержек для некоторых меток в таблице занятости. Число меток в строке не изменяется. Каждая задержка передвигает метку на один период синхронизации вправо. Положение задержек выбирается так, чтобы каждая строка таблицы занятости соответствовала некоторому классу совместимости того цикла, который должен по желанию разработчика соответствовать таблице занятости.
Имеются два типа задержек: входные и выходные. Входная задержка на единицу времени эквивалентна введению дополнительной ступени холостой логике непосредственно перед логикой данной ступени. Аналогично выходная задержка, на единицу времени эквивалентна добавленной ступени холостой логике сразу после логике данной ступени. Выходная задержка на некоторой ступени, очевидно, эквивалентна входной задержке для остальной части логике. Так же задержка может быть реализована путем добавления логики, или, что делается чаще, использованием двухпортовых регистровых файлов с последующим управлением адресами, поступающими на каждый порт. Последний подход распространен гораздо шире, так как он позволяет микропрограммным способом гибко управлять длительностью задержки, вводимой по мере надобности.
Входные задержки в одной строке могут вызвать входные и выходные задержки меток в других строках. Вопрос о том, требуются они или нет, зависит от факторов, не поддающихся учету внутри самой таблицы занятости, таких, как зависимость входа одной ступени от выхода другой. Это, в свою очередь, зависит от того, каким образом функции, выполняемые ступенями, взаимодействуют на уровне исходной задачи.
Цикл (1,5); <1,5,1,5,1,5,…..>последняя латентность
[0,1,6,7,12,13,18,19,24,….] последние инициации
[1,5,6,7,11,12,…] -Gc
[1.5]-Gc mod6
[0.2.3.4] -Hc mod6
При определенных случаях любую таблицу замен, с зависимостями между строками, можно так модифицировать, чтобы она допускала произвольным циклам в качестве последовательности инициаций. Ключ к этому дает следующая теорема:
Теорема. Пусть даны произвольные классы совместимости для произвольного цикла и произвольная строка таблиц замен, такая, что число меток в этой строке равна числу элементов в классе совместимости. Тогда, в предположении, что зависимостей между строками нет, к рассматриваемой строке всегда могут быть добавлены достаточные задержки с тем, чтобы она стала соответствовать этому классу совместимости или модификации этого класса.
Доказательства приводится путем следующего построения. Пусть метки в строках приходятся на индексы а(1), а(2),… и пусть с(1),с(2),… значения, вход в класс совместимости (не обязателен в порядке возрастания). Начнем с первого элемента или множества. Если а(1)< c(1), то вставим с(1)-а(1) входных задержек перед первой меткой в этой строке; все метки справа тоже передвинутся на с(1)-а(1) позиций вправо.
Если а(1)>с(1), то а(1)-с(1)складывается с любым элементом класса совместимости по mod P ( Р- период цикла ), что создает новый, но эквивалентный класс используемый в дальнейшем, оставшиеся метки просматривают, затем слева на право. Если а(i)< c(i), i-я метка задерживается на с(i)-а(i) синхроимпульсы, а все метки в этой строке справа от i-й, передвигаются вправо. Если же а(i)>с(i), то достаточно большое краткое периода цикла Р добавляется к с(i), чтобы отправить это неравенство. Метка а(i) задерживается затем на соответствующую разность.
Пример (рисунок 12.22).
Пусть задана следующая таблица занятости:
| х | х | х | ||||
| х | х | х | ||||
| х | х |
Граница латентности=3
Оптимальный цикл=(4)
MAL=4
Время вычисления =6
Запрещенные латентности {0,1,2,3,5}
Вектор столкновений =111101
(4)
|
Рисунок 12.22.
То есть оптимальным является цикл (4), нижняя граница латентности равна 3 и латентность не достигает нижней границы.
Возьмем цикл (1,5).
Цикл (1,5); <1,5,1,5,1,5,…..>- последовательность латентностей.
[0,1,6,7,12,13,18,19,24,….] - последовательность инициаций.
[1,5,6,7,11,12,…] –множество Gc
[1,5]- множество Gc mod6
[0,2,3,4] - множество Hc mod6
Для цикла (1,5) Hc mod6 равно {0,2,3,4}. Используя приведенный выше алгоритм, определим все совместимые подмножества (Рис.12.23).
Рисунок 12.23.
В число максимальных классов совместимости цикла входят классы{0.2.4},{0,3}.
Модифицируем таблицу занятости в соответствии с классами совместимости. В первой строке таблиц занятости стоят три метки в позициях{0,2,5}. При сравнении с классом {0,2,4} обнаруживаем, что первые 2 элемента уже совпадают а(1)=0=с(1) и а(2)=2=с(2). Но с(3)=4 меньше а(3)=5. Прибавление периода Р=6 к с(3) дает 10-число больше чем а(3).Задержка а(3) на 5 периодов синхронизации дает первую строку матрицы. В строке 2 а(1)=1 больше чем с(1) из {0,2,4}. Поэтому мы строим эквивалентный класс совместимости{1,3,5} и задерживаем вторую метку на один такт. Третья метка становится на свое место. Третья строка таблицы замен приводится к классу {2,4} путем задержки на один такт второй метки. Заметим, что{2,4} не только подмножество {0,2,4}, но еще и класс совместимости.
Хотя возможны другие схемы задержек, это обладает явным преимуществом, так как дает правильную вычислительную последовательность, независимо от того, какие межстроковые зависимости существуют.
В результате получим следующую таблицу занятости (рисунок 12.24):
| х | х | d | d | d | d | d | d | х | |||
| х | d | х | х | ||||||||
| х | d | х |
Граница=3
Оптимальный цикл = (1,5)
MAL=3
Время вычисления=11
d – задержка
Рисунок 12.24.
Описанная структура позволяет разработчику теоретически выбрать любой цикл, средняя латентность которого не меньше, чем максимальное число меток в строке и откорректировать затем таблицу занятости так, чтобы она допускала этот цикл. Сюда относятся и постоянные циклы, в частности, постоянные циклы (L), где L=max числу меток в строках таблицы. Такие циклы совершенны, что приводит к таблицам занятости, у которых MAL достигает нижней границы и у которых хотя бы одна ступень конвейера используется на 100%.
Хотя все это теоретически возможно, в реальных системах встречаются ограничения, которые препятствуют достижению оптимальной производительности:
1) Не всегда фиксаторы являются регистровыми файлами ( несущественное ограничение - всегда можно обойти).
2) Задержка на один такт требует одного регистра в файле. Поэтому когда число ступеней велико, период типичного цикла также проявляет тенденцию к увеличению, задержка может быть близка к периоду и файла может не хватить.
Это должно учитываться при разработке конвейера.
Дата добавления: 2015-08-14; просмотров: 989;
