Диаграмма состояний.

Цель стратегии управления состоит в том, чтобы определить, когда осуществлять новые инициации, не приводящие к столкновениям с прежними инициациями. Одним из методов выявления и представления такой информации является метод, основанный на диаграмме состояний, в которой текущей конфигурации конвейера для каждого момента времени соответствует одно из состояний. Дуги, идущие от одного состояния к последующим, показывают, в каком из новых состояний конвейер может находиться в следующий момент времени. Все возможные последовательности латентностей соответствуют путям на такой диаграмме. Анализируя все пути, особенно те, которые образуют замкнутые циклы, можно определить пути с минимальной средней латентностью. Тогда последовательности латентностей, которым эти пути соответствуют, являются оптимальными.

В любом состояний закодированная информация называется вектором столкновений. Такой вектор является d – разрядно двоичной последовательностью, где d – время вычисления для таблицы занятости. При этом d разрядов нумеруются от 0 до d-1 слева направо, при этом 0 в i-ой позиции означает, что у инициации, начатой через i единиц времени после текущего момента, не будет столкновений ни с одной из незавершенных в текущий момент инициации, а 1 означает, что столкновения будут и поэтому инициация должна будет запрещена. В векторе столкновений для любого периода времени учитывается, будет ли новая инициация в этом периоде.

Вектор столкновений для начального состояния называется начальным вектором столкновений. Поскольку он соответствует моменту времени начального запуска конвейера, то он определяет, какие латентности вообще допустимы только между двумя инициациями: в моменты 0 и i. Он определяет также допустимую латентность между любыми двумя инициациями без учета ранних действий конвейера. Вычисление начального вектора столкновений производится непосредственно. Для любого значения i между 0 и d-1 копия таблица занятости сдвигается на i единиц времени вправо и накладывается на несдивагаемую копию таблицы. Если где-либо в пределах наложения таблиц в одной графе «время- ступень» оказываются 2 метки, то i-й разряд начального вектора столкновений полагается равным 1, в противном случае 0. Во всех случаях нулевой разряд вектора столкновений равен 1, поскольку наложение таблицы занятости самой на себя приводит к столкновению во всех графах, содержащих метки. Аналогично, во всех разрядах, начиная с d, всегда стоят нули, поскольку сдвинутая и несдвинутая таблицы не перекрываются. Так как это имеет место всегда, нет необходимости представлять эти разряды в векторе столкновений.

Альтернативный подход состоит в построении множества запрещенных латентностей. Число i является членом этого множества в том и только в том случае, когда хотя бы в одной строке таблицы занятости имеются 2 метки, разделенные i столбцами. С помощью анализа меток в любой строке быстро определяется все члены множества, 0 всегда ему принадлежит. Для всех i принадлежащему этому множеству, соответствующий разряд в начальном векторе столкновений равен 1. Все остальные разряды равны 0. Например, для таблицы В множество запрещенных латентностей равно {0,1,2,5,6,7,}, а соответствующий вектор столкновении равен 11100111.

Если начальное состояние конвейера в момент времени 0 известно, что можно вычислять эквивалентные состояния для всех будущих моментов времени. Если вектор столкновении в момент времени t известен , то вектор столкновений для t+1 вычисляется по следующей процедуре.

Генерирование диаграммы состояний:

1. Вектор столкновений для момента времени t сдвигается влево на 1 разряд, самый левый разряд отбрасывается, а в правый разряд заносится 0.

2. Если в нулевом разряде этого вектора содержится 1, то это новый вектор столкновений.

3. Если в нулевом разряде содержится 0, то в момент t+1 возможны два состояния в зависимости от того, произведена ли новая инициация в момент t+1. Если инициация не произведена, то сдвинутый вектор столкновений представляет очередное состояние. Если же в момент t+1 произведена инициация, то новый вектор столкновений является результатом поразрядной логической операции ИЛИ, сдвинутого вектора и копии начального вектора столкновений.

4. Во всех случаях, когда новый вектор столкновений идентичен вектору для одного из предыдущего состояния, дуга от текущего состояния возвращается к этому предыдущему. Если же вектор столкновений является новым, то определяется новое состояние и проводится дуга от старого состояния к новому. Дуги, соответствующие единице времени, в которой производится новые инициации помечаются знаком каким либо знаком (например *).

Правильность процедуры вытекает из следующего: если в момент времени t вектор столкновений имеет единицу в i разряде, то необходимо избегать инициации в момент t+1. Следовательно, вектор столкновений в момент t+1 должен учитывать это, но тогда требуется, чтобы в разряде i-1 для момента t+1 стояла единица. Если в момент t+1 не производится новая инициация, то верно и обратное, а именно, в разряде i-1 стоит единица, только если в момент t стояла единица. Этим оправдываются шаги 1 и 2.

Шаг 3 учитывает возможность инициации в момент t+1. Это имеет место, только если в момент t в разряде 1 вектора столкновения стоял 0 (или в момент t+1 в результате шага 1 в разряде 0 стоял 0). Если эта диаграмма должна охватить все возможные последовательности латентности, то, следовательно, нужно рассматривать обе возможности, то есть выполнение и невыполнение инициации. Это требует введения двух дуг исходящих из состояния соответствующему моменту времени t. Разумеется, всякая последовательность латентностей «пойдет» лишь по одной из них. Первая дуга относится к случаю, когда инициация не выполняется. Здесь вектор столкновений в момент t+1 будет вектор, полученный на шаге 1. Вторая дуга относится к новой инициации в момент t+1. В этом случае всякая дальнейшая инициация, выполняемая после момента t+1, должна избегать столкновений, как с инициациями, выполненными до момента t+1, так и с инициацией, произведенной в момент t+1. Но эти последние столкновения полностью определяются копией начального вектора столкновения. Связывание его операцией логического ИЛИ со сдвинутым вектором дает вектор , перечисляющий те и только те будущие моменты времени, в котором может наступить столкновений какого либо из этих двух видов.

Шаг 4 сохраняет диаграмму в виде конечного замкнутого графа, так как новые состояния могут быть идентичны состояниям полученным ранее.

Для таблицы занятости В диаграмма состояний имеет следующий вид (рисунок 12.17):

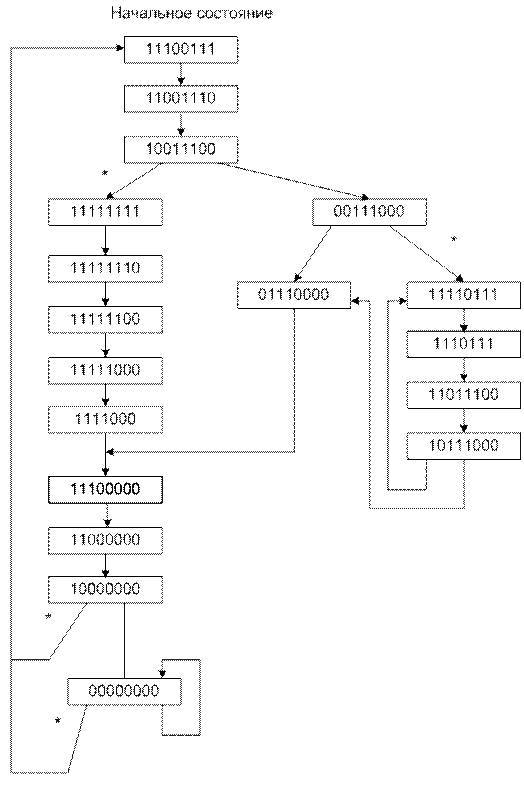
Рисунок 12.17.

В диаграмме имеются циклы , например цикл(4), в котором через любые четыре такта может быть выполнена новая инициация. В диаграмме также имеются циклы (3,8), (3,9), (3,10), (8), (4,8,3,8).

Модифицированная диаграмма состояний.

Даже для простых таблиц занятости диаграмма состояний сложна. Поэтому строят модифицированную диаграмму состояний, которая содержит только состояния, возникающие при новых инициациях.

В исходной диаграмме это состояние помечено (*) на одной из входных дуг. Два состояния на новой диаграмме соединяется дугой только в том случае, если в исходной диаграмме они были соединены серией дуг, из которой последняя помечена (*). Кроме того, эта дуга в новой диаграмме помечена числом, соответствующий числу дуг между двумя состояниями в исходной диаграмме. Это число есть латентность между двумя инициациями.

На рисунке 12.18 представлена модифицированная диаграмма.

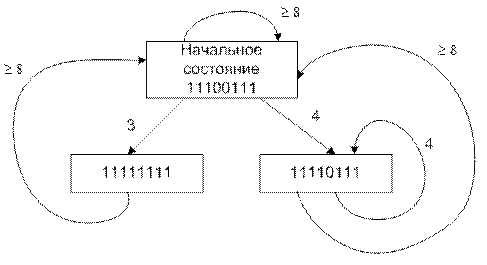
Рисунок 12.18.

Модифицированная диаграмма содержит всю существенную информацию, содержащуюся в исходной. Имеется однозначное соответствие между циклами двух графов. Правильные последовательности латентностей представляет собой просто списки значений на дугах. Средняя латентность цикла и последовательности получается непосредственно суммированием латентностей по циклу и подсчетом числа состояний. Единственная информация которая сюда не включается - векторы столкновений для состояний, в которых инициации не выполняются.

Процедура генерирования модифицированной диаграммы состояний:

1. В качестве начального состояния диаграммы принять начальный вектор столкновений.

2. Для любого необработанного состояния и каждого к такого, что к-й разряд соответствующего вектора столкновения равен 0 выполнить следующие шаги:

a) сдвинуть вектор столкновений на к разрядов влево, отбросив первые к разрядов и добавив к нулей справа;

b) произвести операцию логического ИЛИ с копией начального вектора столкновений;

c) полученное новое состояние соединить с текущим состоянием дугой с меткой к.

3. Добавить дугу с меткой ≥ d от любого состояния назад к начальному состоянию, где d – время вычисления для таблицы занятости.

Для простоты дуги, задействованные на шаге 3 , не показываются, а часто просто подразумеваются. Правильность этой процедуры непосредственно вытекает из предыдущего.

Модифицированная диаграмма состояний представляет в компактной форме все возможные последовательности инициаций. Основная цель оптимальной диспетчеризации – выбрать из них ту последовательность и те последовательности, которые обеспечивают максимальную возможность производительность и наименьшую MAL. Если число инициаций, которые надо сделать сравнительно мало, то допустим исчерпывающий перебор всех возможных путей. Однако, если в конвейере осуществляется инициация некоторого вида сколь угодно больше число раз, то исчерпывающий перебор становится невозможным. Необходимо более конструктивный подход.

На основе анализа циклов в модифицированной диаграмме состояний, можно построить эффективный алгоритм диспетчеризации. При неограниченно длинных сериях инициаций, но при конечном числе состояний любая последовательность инициации будет, в конце концов, образовывать циклы. Поскольку, средняя латентность цикла, повторенного много раз, является просто средней латентностью самого цикла (период/число дуг), оптимальный алгоритм должен только перечислять все возможные циклы в диаграмме состояний и выбрать среди них те, которые имеют минимальную среднюю латентность (MAL). Само оптимальное расписание будет в этом случае состоять из минимальной по времени последовательности инициаций, ведущей от начала состояния к любому из состояний в одном из этих минимальных циклов, за которым будет следовать повторяющееся использование этого цикла. Для цикла, последовательность латентностей (цикл латентностей) записывается в виде перечня латентностей в скобках.

Простой цикл – цикл, в котором любое состояние проходится не более одного раза за одно повторение цикла.

Лемма. Если в произвольной модифицированной диаграмме состояний имеется цикл с средней латентностью L, то имеется по меньшей мере один простой цикл со средней латентностью не большей L.

Если этот цикл простой, то лемма тривиальна. Если же он не является простым, то представляет собой некоторую комбинацию простых циклов. Допустим, цикл состоит из m простых циклов, из которых i -й проходится К(i) раз и имеет период Р(i) с S(i) состояниями ( период цикла – сумма латентностей). Тогда средняя латентность определяется выражением:

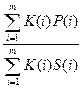
Если бы лемма была ложной, то латентности всех простых циклов должны были бы превышать это среднее, то есть:

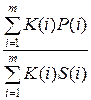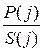< , для любого j

Выберем цикл r так, чтобы латентность P(r)/S(r) была наименьшей по всем i, тогда

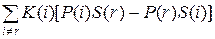< 0

Так как K(i) ≥ 0 для любого i, то хотя бы один из членов должен быть отрицательным:

P(i)S(r)-P(r)S(i) < 0

Если это имеет место для i, то P(i)S(r)< P(r)S(i), что противоречит предположению относительно r. (Получается, что < .)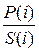

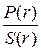Лемма позволяет ограничить поиск оптимальных циклов простыми циклами. Хотя область поиска оптимальных стратегий уменьшилась, однако объем работы для сложной диаграммы состояния все еще велик. При некоторых условиях можно перечислить только жадные циклы, в которых в качестве дуги, выходящей из любого состояния выбирается дуга с минимальной латентностью.

Процедура определения всех жадных циклов следующая :

1. Выбрать любое состояние из модифицированной диаграммы состояний.

2. Идти по последовательности дуг минимальной латентности, пока не встретится состояние, выбранное на шаге 1, либо пока не останется больше дуг.

3. В первом случае последовательность является жадным циклом. Ее надо записать, а все входящие в нее состояния исключить из диаграммы.

4. Выбрать другое состояние и вернуться к шагу 2.

Правильность процедуры очевидна. Ей требуется самое большое N итераций, где N – число состояний диаграммы.

Лемма Средняя латентность любого жадного простого цикла меньше или равно числу единиц в начальном векторе столкновений. Пусть состояния составляющие жадный цикл обозначаются S(1), S(2), .., S(m), а дуги имеют латентности L(1),L(2), .., L(m) (рисунок 12.19).

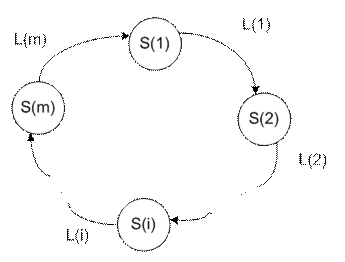
Рисунок 12.19.

Пусть х(i) – общее число единиц в векторе столкновений для состояния S(i), Х – число единиц в начальном векторе столкновений. Для жадного цикла вектор столкновений для S(i) должен иметь L(i) левых единиц, за которым следует 0, в противном случае эта дуга не является жадной. Таким образом, в векторе столкновений для S(i+1) имеется самое большое х(i)- L(i) единиц из сдвинутого вектора для S(i) и Х единиц из копии начального вектора столкновений, то есть:

x(i+1) ≤ x(i)-L(i)+x

Тогда получим:

x(2) ≤ x(1)-L(1)+x

x(3) ≤ x(2)-L(2)+x ≤ x(1)-L(1)-L(2)+2x

…

x(m) ≤ x(m-1)-L(m-1)+x ≤ x(1)-L(1)- … - L(m-1)+ (m-1)x

Для замыкающей дуги получим:

x(1) ≤ x(m)-L(m)+x

или

x(1) ≤ x(1) - + mx

Отсюда:

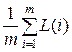= x

Левая часть – средняя латентность для данного цикла, а правая- число единиц в начальном векторе столкновений.

Эта лемма устанавливает верхнюю границу для средней латентности любого жадного цикла. Ранее доказанная лемма установила нижнюю границу для средней латентности любого цикла. Из этих лемм имеем :

Максимальное число меток в любой строке таблицы занятости ≤ MAL;

MAL ≤ средняя латентность любого жадного цикла(т.к. жадная стратегия не всегда оптимальна);

Средняя латентность любого жадного цикла ≤ число единиц в начальном векторе столкновений.

Таким образом:

Максимальное число меток в любой строке ≤ MAL ≤ число единиц в начальном векторе столкновений

Отсюда можно сразу определить, является ли данный жадный цикл оптимальный. Если максимальное число меток в строках таблицы занятости равно числу единиц в начальном векторе столкновений, то все жадные циклы оптимальные и любой из них может быть выбран.

Если эти границы не равны, но какой-либо жадный цикл имеет среднюю латентность равную нижней границе (число меток), то он является оптимальным циклам.

Однако эти границы и жадные циклы не всегда непосредственно определяют оптимальный цикл. Может быть случай, когда нижняя граница недостижима и значение MAL больше ее или случай, когда среди жадных циклов нет оптимальных. В этих случаях надо просмотреть все циклы.

В литературе имеются таблицы, в которых приведен перечень всех достижимых MAL для всех векторов столкновений из 9 и менее разрядов, а также все жадные и все оптимальные циклы.