Отношения между нечеткими множествами.

Пусть – непустые множества и предметная область Х – есть декартово произведение Х = . Нечетким n-арным отношением Р, заданным на области определения Х, называется нечеткое множество следующего вида:

Р = {(( 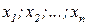); ( 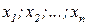)):( ) 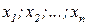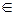Х }, (9.13)

где ( 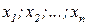): - функция принадлежности для элементов n-арного отношения Р.

Пример. Х = 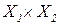, где 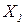= {1;2;3;4;5}; 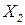= {1;2;3;4}. На множестве

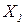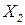
		0,35	0,2
	0,2	0,1		0,8
	0,13			0,91	0,75
	0,7			0,45	0,56

Х определено нечеткое бинарное

отношение 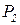с функцией принад-

лежности 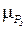, заданной таблично.

Определим явный вид заданного нечеткого бинарного отношения .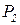

По определению (9.13) в данном случае следует записать:

.

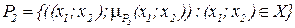Подставляя в полученное выражение данные таблицы находим явный вид :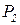

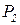={(1;2)/0,2;(1;3)/0,13;(1;4)/0,7;(2;1)/0,35;(2;2)/0,1;(3;1)0,2;(4;2)/0,8; (4;3)/0,91;(4;4)/0,45;(5;3)/0,75;(5;4)/0,56},

где принята запись ~ ( )/ .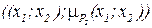

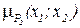Частным случаем нечеткого бинарного отношения является нечеткая импликация, которая определяется следующим образом. Пусть А и В – нечеткие множества, заданные своими функциями принадлежности 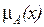, 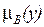на областях определения X,Y. Нечеткая импликация А 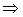В (если А, то В) по Мамдани [10] основана на предположении, что степень истинности заключения 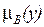не может быть выше, чем степень выполнения условия 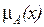, т.е.: 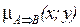= min ( 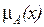; 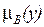) (9.14)

Интуитивно такое предположение вполне понятно, например, из следующего правила: ЕСЛИ (автомобиль = новый), ТО (расход топлива = малый). Это правило представляется почти очевидным и, таким образом, нечеткая импликация является основой нечеткого логического вывода.