Нечеткий вывод в системе принятия решений.

Нечеткий логический вывод довольно часто используется в задачах управления, включая принятие ответственных решений. В частности, такой подход довольно успешно применяется в задачах классификации, примером которой является оценка клиентов, заинтересованных в получении кредита. Если клиент достаточно кредитоспособен, то банк с большей готовностью выдаст ему кредит и может уменьшить процентную ставку; если клиент не является кредитоспособным, то в выдаче кредита ему будет отказано; и, в случае частичной кредитоспособности клиента, банк выдаст ему ограниченную сумму и, возможно, повысит процентную ставку. Таким образом, вводится классификация клиентов на кредитоспособных (КС), частично кредитоспособных (ЧКС) и некредитоспособных (НКС).

Введенные понятия классификации, очевидно, являются нечеткими и, следовательно, требуют введения степеней принадлежности к тому или иному классу клиентов, используя их кредитные истории. Клиентов, погасивших кредит в установленный срок и в полном объеме относят к классу КС; клиентов, не погасивших кредит в полном объеме – к классу НКС, а клиентов, погасивших кредит не в установленный срок – к классу ЧКС. Помимо этого, для получения кредита клиент должен предоставить банку определенную информацию, например:

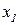– среднюю величину полного дохода;

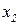– количество материально зависимых лиц (иждивенцев);

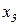– объем имеющихся долгов;

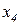– оценка стоимости его активов;

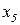– период занятости на текущем месте работы;

– период занятости на предыдущих местах работы;

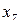– запрашиваемая сумма кредита.

Эти данные на каждого клиента в виде вектора ( 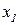; ; 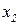; ; 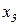; ; 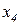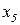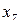) вводятся в соответствующую банковскую базу данных и далее на основе имеющейся предыстории клиентов экспертом банка строится необходимая для принятия решения классификация по степеням принадлежностей клиентов 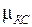; ; 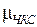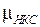. Схема нечеткого классификатора клиентов банка представлена на рис. 9.2.

Рис. 9.2.

Следует отметить, что оценка кредитоспособности клиентов является сложной задачей, которая связана с обработкой больших массивов данных (в реальности, далеко выходящего за пределы 7 показателей). Поэтому для ее решения обычно создают автоматический классификатор, который может обучаться на основе данных о предыдущих клиентах банка, а затем использоваться для оценки будущих клиентов.

В целом, процесс построения нечеткой лингвистической модели реальной системы представлен на рис.9.3.

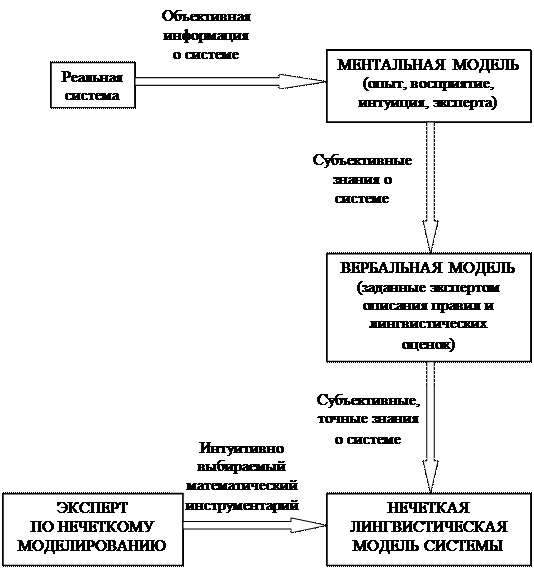Рис.9.3. Построение нечеткой лингвистической

модели реальной системы

Библиография к части 2.

1. Искусственный интеллект. Справочник. В 3-х кн. Кн. 2. Модели и методы: / Под ред. Д.А. Поспелова. – М.: Радио и связь, 1990. – 304 с.

2. Приобретение знаний / Под ред. С. Осуги, Ю. Саэки. – М.: Мир, 1990. – 304 с.

3. Anderson R. John. The architecture of cognition. – Cambridge (Massachusetts, USA): Harvard Univ. Press, 1983. – 163 p.

4. Барвайс Дж. Введение в логику первого порядка // Справочная книга по математической логике. Часть I: Теория моделей. – М.: Наука, 1982. – С. 13-54.

5. Игошин В.И. Математическая логика и теория алгоритмов. – М.: Издательский центр «Академия», 2004. – 448 с.

6. Поспелов Д.А. Логико-лингвистические модели в системах управления.– М.: Энергоиздат, 1981. - 231 с.

7. Вагин В.Н., Кикнадзе В.Г. Дедуктивный вывод на семантических сетях в системах принятия решения // Изв. АН СССР: Техническая кибернетика, 1984, № 5. – С. 104-120.

8, Фирстов В.Е. Информационно-стохастическая модель и оптимизация при построении и распространении математического знания. – Саратов: ООО Издательство «Научная книга», 2006. – 55с.

9. Зиман Э., Бьюнеман О. Толерантные пространства и мозг // В кн. На пути к теоретической биологии. – М.: Мир, 1970. – С. 134-144.

10. Пегат А. Нечеткое моделирование и управление. – М.: БИНОМ, Лаборатория знаний, 2009. – 798 с.

11. Заде Л. Понятие лингвистической переменной и его применение к принятию приближенных решений. – М.:Мир,1976.–165 с.

12. von Altrock C., Krause B., Zimmerman H.J. Advanced fuzzy logic control of a model car in extreme situations // Fuzzy Sets and Systems, 1992, vol.48, №1. – P. 41-52.

13. Bezdek J.C. Editorial. Fuzzy models – what are they, and why? // IEEE Transactions on Fuzzy Systems, 1993, vol.1, №1. – P.1-6.