Нечеткое множество и его характеристики.
Нечетким множеством А. определенным на некоторой числовой предметной области Х, называется множество пар [10]:
А = {( 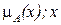 ):
): 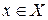 }, (9.1)
}, (9.1)
где 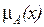 – степень принадлежности элемента
– степень принадлежности элемента 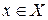 , представляющая функцию
, представляющая функцию 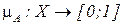 . Функция принадлежности может задаваться графически, аналитически или таблично, При аналитическом задании функцию
. Функция принадлежности может задаваться графически, аналитически или таблично, При аналитическом задании функцию 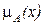 обычно используют следующие аппроксимации: линейную, полиномиальную, гауссову (нормальную), сигмоидальную и др.
обычно используют следующие аппроксимации: линейную, полиномиальную, гауссову (нормальную), сигмоидальную и др.
Нечеткое множество А, у которого функция принадлежности 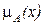 = 0 во всей области Х , называется пустым А =
= 0 во всей области Х , называется пустым А =  . Если для всех элементов предметной области
. Если для всех элементов предметной области 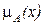 =1, то такое нечеткое множество называется универсальным и обозначается символом U.
=1, то такое нечеткое множество называется универсальным и обозначается символом U.
Равенство нечетких множеств А и В определяется соотношением:
А = В 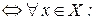 (
( 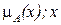 )=(
)=( 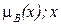 ). (9.2)
). (9.2)
Очевидно, равенство нечетких множеств (9.2) обладает свойствами рефлексивности (А=А); симметричности (А=В 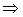 В=А) и транзитивности (А=В
В=А) и транзитивности (А=В 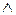 В=С
В=С 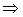 А=С).
А=С).
Введение подмножества(отношения включения) для нечетких множеств определяется соотношением:
А 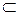 В
В 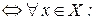 (
( 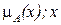 )
) 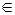 А
А 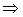 (
( 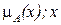 )
) 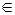 В,(9.3)
В,(9.3)
где 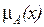
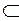
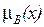 . Отношение включения (9.3) рефлексивно (А
. Отношение включения (9.3) рефлексивно (А 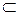 А), транзитивно (А
А), транзитивно (А 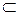 В
В 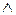 В
В 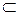 С
С 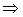 А
А 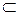 С) и антисимметрично (А
С) и антисимметрично (А 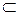 В
В 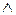 В
В 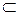 А
А 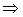 А=В).
А=В).
Наиболее распространенными характеристиками нечеткого множества А являются следующие:
высота нечеткого множества, определяемая как верхняя грань значений, принимаемых функцией принадлежности в области Х:
h(A) = sup ( 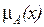 ),
), 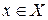 ; (9.4)
; (9.4)
носитель нечеткого множества – подмножество области Х, содержащее элементы, степень принадлежности которых отлична от 0:
S(A) = Carr(A) = {x: 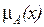 > 0,
> 0, 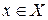 }; (9.5)
}; (9.5)
ядро нечеткого множества – подмножество области Х, элементы которого имеют степень принадлежности 1:
C(A) = Ker(A) = {x: 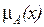 > 0,
> 0, 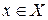 }; (9.6)
}; (9.6)
вертикальное представление нечеткого множества – это множество пар ( 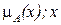 ) на декартовой плоскости. Пример вертикального представле-ния нечеткого множества представлен на рис.9.1.
) на декартовой плоскости. Пример вертикального представле-ния нечеткого множества представлен на рис.9.1.
 | |||||||||
| |||||||||
 | |||||||||
 |  |
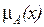
| 0,25 | 0,5 | 0,75 | 0,5 | |||
| х |
Рис.9.1. Пример вертикального представления дискретного
нечеткого множества.
Замечание. В некоторых случаях не удается определить степень принадлежности точно, в числовой форме, как это сделано в определении (9.1).Иногда это можно сделать только лингвистически, используя нечеткую меру. В этом случае функция принадлежности принимает вид 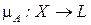 , где L – множество нечетких значений степени принадлежности, и тогда множество А иногда называют нечетким множеством 2-го рода [10].
, где L – множество нечетких значений степени принадлежности, и тогда множество А иногда называют нечетким множеством 2-го рода [10].
Дата добавления: 2015-08-14; просмотров: 983;
