Дедуктивный вывод на семантических сетях.

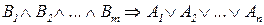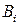Семантическая сеть, как отмечалось (п.6.2.1), представляет собой информационную модель предметной области знаний, которая включает факты и общие закономерности (аксиомы, посылки). В рамках логико-лингвистической модели [6] с каждой семантической сетью сопоставлена совокупность дизъюнктов вида: (что равно-сильно: ), где – условия ( 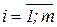), 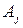– заключения ( 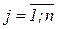). В семантической сети имеются два вида вершин – предикатные и дизъюнктные (коммутаторы) так, что предикатные вершины связаны между собой дугами только через коммутаторы [8],

Задача дедуктивного вывода в этом случае формулируется следующим образом. Дана логико-лингвистическая модель в виде семантической сети, с которой сопоставлен набор дизъюнктов указанного типа, и на ее вход подается ситуация, представленная совокупностью фактов 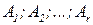. Эта ситуация, накладываемая на семантическую сеть, представляет собой текущее состояние системы обработки знаний, отражающее динамику ее изменения. Кроме того, на вход модели подается запрос, также приведенный к виду дизъюнктов.

Решение задачи дедукции состоит в получении противоречий в семантической сети по аналогии с установлением противоречия в принципе резолюции (п.8.2). Отметим, что в логико-лингвистической модели [6;7] процедура дедуктивного вывода основана на использовании многосортной логики предикатов 1-го порядка, что позволяет существенно ограничить область поиска необходимых утверждений, хотя сортность переменных может быть исключена введением соответствующих одноместных предикатов.

Среди алгоритмов уменьшения перебора при поиске нужной информации, а также быстрого и эффективного извлечения информации особо рассмотрим алгоритм, связанный с ракраской вершин данной семантической сети [7]. Правило раскраски следующее: в дизъюнкте В 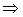А условие В будет раскрашено цветом 1, а заключение А – цветом 2, причем, поскольку вершины В и А соединены дугой через коммутатор g, то дуга до него изображается сплошной линией, а после него – пунктирной.

Пример. Для дизъюнкта 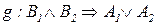имеем дизъюнктную вершину g (коммутатор), четыре предикатные вершины 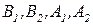и четыре дуги: две непрерывные, идущие от вершины g к 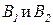, и две пунктирные, идущие от g к .

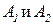Алгоритм дедукции на раскрашенных семантических сетях состоит в следующем [7]. Для предикатной вершины В подбирается любая контрарная пара (g;A), резольвирующая дизъюнкт g: В 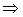А. Если исходная вершина В имеет другие контрарные пары, то они рассматриваются как альтернативные, но их выбор происходит только после неудачи с унификацией текущей контрарной пары (g;A). Если в вершину входят дуги только одного цвета, то они удаляются из рассмотрения, поскольку не влияют на вывод пустой сети (т.е. противоречия). Процесс продолжается до тех пор, пока не будет выявлена пустая сеть. Данный алгоритм позволяет обрабатывать сети большой размерности, однако он эффективен и полон только в таких системах обработки знаний, которые описываются набором хорновских дизъюнктов.

Лекция 9. Нечеткий вывод на знаниях.