Правило вывода по принципу резолюций.

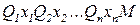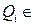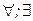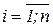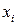В методе резолюции [5] исходная логическая формула приводится к специальному виду, называемому пренексной нормальной формой (ПНФ), имеющей вид: , где { }, , - предикатные переменные, М – бескванторная формула представленная в виде конъюнктивной нормальной формы (КНФ). С помощью функций Т. Сколема в данной ПНФ, сохраняя ее общезначимость, можно устранить кванторы существования и в итоге получаем стандартную форму.

Пример. Логическую формулу 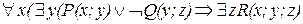привести к стандартной форме.

Преобразуем данную формулу в ПНФ:

= =

= =

= .

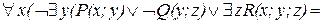
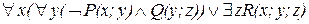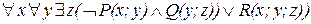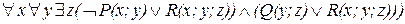Для устранения квантора введем функцию Сколема z=f(x;y). В результате получаем искомую стандартную форму в виде:

.

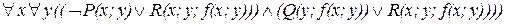Обычно в стандартной форме ПНФ кванторы общности опускают, предполагая, что все переменные ими связанные являются универсально квантифицированными. Поэтому любая формула может быть представлена множеством дизъюнктов. В частности, в разобранном примере множество дизъюнктов S = { 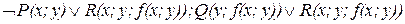}, где запятая между дизъюнктами заменяет знак .

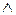Из разобранного примера следует, что в методе резолюций общезначимость логической формулы устанавливается путем анализа множества дизъюнктов S: если оно не содержит ложных дизъюнктов, то ответ положительный; в противном случае данная формула общезначимой не является.