Внешние характеристики.

К внешним характеристикам турбинной ступени (турбины) относят мощность N, крутящий момент на валу M, число оборотов ротора n, расход рабочего тела G, располагаемая работа L₀, КПД и др. Графическая взаимосвязь между любыми двумя из этих величин называется характеристикой ступени (турбины).Рассмотрим связь между наиболее важными (итоговыми) внешними характеристиками: мощностью N, моментом M и частотой вращения n. При неизменном положении органов управления и регулирования сохраняются постоянными расход рабочего тела G=G₀ и располагаемая работа L₀=L₀₀. Изменяя нагрузку потребителя механической энергии, произойдет торможение (уменьшение n) или разгон (увеличение n) системы ротор турбины – потребитель. Такая ситуация имеет место при изменении угла установки лопастей ВРШ.

Для крутящего момента можно записать

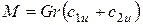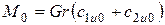; (5.19)

где r – средний радиус лопаток.

Из треугольников скоростей (рис.13)

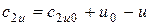, тогда

,

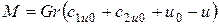в этой формуле учтено допущение, что с_1u=c_1u0.

Очевидно, что при u=u₀ получим момент М₀ на номинальном режиме. При неподвижной турбине достигается наибольшее значение момента

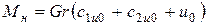. (5.20)

Так как 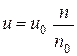, то

. (5.21)

Введем относительные значения характеристик

, , .

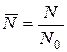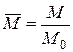Коэффициент пускового момента называется отношение

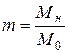. (5.22)

Учитывая, что 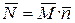из уравнения (5.21) находим

, (5.23)

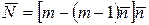. (5.24)

Пренебрегая изменением механических потерь энергии, потерь в решетках, потерь внутренних, а также принимая неизменными расход G и располагаемую работу L₀ получим

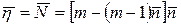. (5.25)

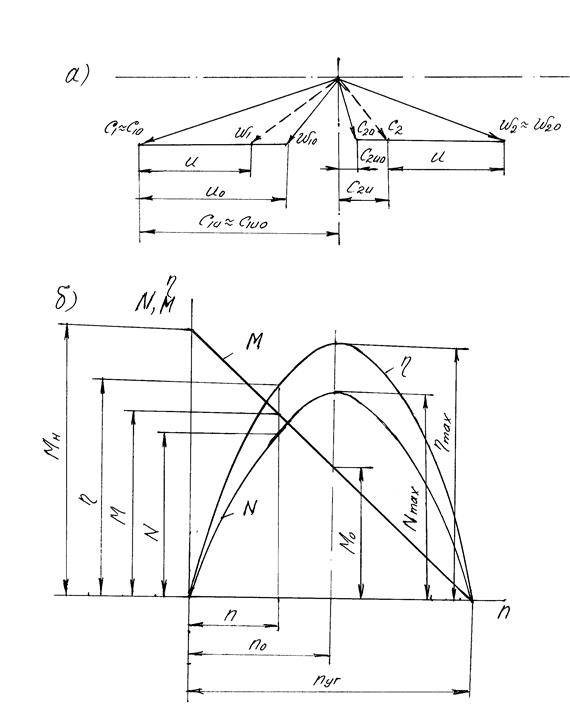
Рис. 13 Работа турбинной ступени с переменными оборотами (G = const, L₀ = const): а) треугольники скоростей; б) изменение мощности, крутящего момента и КПД в функции частоты вращения.

Из формул (5.24) и (5.25) следует, что при указанных допущениях относительные изменения h и N одинаковы, а кривые 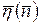и совпадают.

Анализируя полученные выражения можно сделать вывод, что момент есть линейная функция частоты вращения или окружной скорости. Мощность и КПД изменяются по симметричной параболе (рис.13). У рассматриваемых зависимостей есть три особые точки. Первую из них, где мощность и ПД достигают максимального значения, найдем из условия ,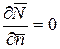

, (5.26)

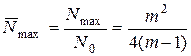. (5.27)

Формулы (5.26) и (5.27) будут справедливы, если n₀ не соответствует максимальной мощности.

Вторая точка соответствует нулевой мощности при вращении турбины, частота вращения при этом называется угонными оборотами n_уг

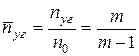. (5.28)

Угонные обороты соответствуют режиму, при котором выходной и входной треугольники скоростей накладываются один на другой (c_1u-c_2u=0).

Ротор турбины устремляется к угонным оборотам при потере нагрузки (поломка муфты, потеря винта и т.п.) Практически угонные обороты на 5¸20% ниже значений, вычисленных по формуле (5.28) из – за увеличения механических и внутренних потерь энергии с повышением n.

Третья особая точа соответствует неподвижному ротору турбины n=0, а момент имеет наибольшее значение определенной формулой (5.21), что возможно при G=G₀ и L₀=L₀₀.