Основные положения расчета на прочность вращающегося диска.

Внешние силы, вызывающие напряжения во вращающемся диске турбомашин: центробежная сила, действующая на диск от закрепленных на нем рабочих лопаток; центробежная сила, возникающая в элементах диска при его вращении.

Рис. 19 . Cxема сил, действующих на элемент диска: у- радиус центра элемента относительно оси вращения; 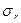- радиальное напряжение на радиусе у; 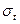- окружное напряжение на том же радиусе; x - ширина диска на радиусе у; w- угловая скорость вращения; r - плотность материала; m=0,3- коэффициент Пуассона.

Диск принят симметричным относительно средней плоскости, поэтому один из 3-х главных компонентов напряжения равен нулю.

Рассмотри условия равновесия бесконечно малого элемента диска (рис.19), образованного двумя цилиндрическими поверхностями, отстоящими друг от друга на расстояние dy и двумя меридиальными плоскостями, расположенными относительно друг друга под бесконечно малым углом dj.

Для равновесия элемента сумма проекции всех действующих сил в радиальном направлении равна нулю. Объем изучаемого элемента yxdjdy, а его центробежная сила rw²y²xdjdy.

По граням 1-2 и 5-6 действует сила со стороны внешнего элемента

,

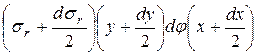а по граням 3-4 и 7-8 – со стороны внутреннего элемента

.

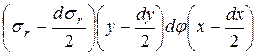По граням 6-7 и 5-8 действуют силы от соседних элементов, расположенных на том же среднем радиусе у. На каждую из этих граней нормально к ней действует сила 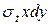, так как напряжение 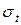приняты постоянными вдоль грани. Радиальная проекция этих сил, направленная к центру диска, равна ,.

После преобразований получим уравнение равновесия элемента

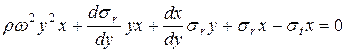. (7.14)

Учитывая, что

,

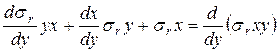уравнение (7.14) можно представить в следующем виде

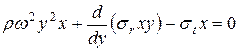. (7.15)

Из теории упругости известно, что связь между напряжениями и полным удлинением диска при радиусе у выражена соотношениями:

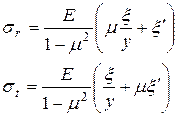(7.16)

В приведенных формулах Е – модуль упругости материала.

Подставляя значения 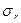и и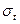з уравнений (7.16) в формулу (7.14) после преобразования получаем

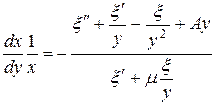, (7.17)

где .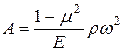

Уравнение (7.17) дает закон изменения относительной толщины диска с изменением радиуса в зависимости от деформации, а следовательно, и от напряжений.

При наличии температурного градиента по радиусу формула (7.17) принимает вид

, (7.18)

где a– коэффициент линейного удлинения.

Точное решение уравнений (7.15) и (7.17) возможно, когда задан аналитический закон изменения х по у. Например для диска постоянной толщины, диска конической или гиперболической формы, диска равного сопротивления.

Для диска постоянной толщины (х=const, dx/dy=0) из уравнения (7.17) для главных напряжений получаем:

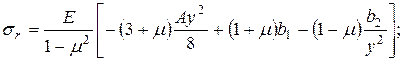(7.19)

(7.20)

Для определения постоянных интегрирования b₁ и b₂ должны быть заданы:

напряжение на наружной поверхности обода от центробежных сил лопаток ;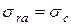

для диска с центральным отверстием на внутренней поверхности , ;

для сплошного диска обе главных напряжения одинаковы , .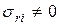

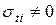При проектировании и расчете следует иметь в виду, что наличие центрального отверстия увеличивает окружные напряжения в центральной части диска приблизительно в 2 раза.

Формулы (7.19) и (7.20) после определения постоянных интегрирования b₁ и b₂ приводят к удобному для расчета диска виду

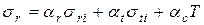; (7.21)

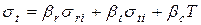, (7.22)

где ;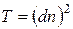

здесь d= 2y, м; n- частота вращения диска об/мин.

Коэффициенты, входящие в уравнение (7.21), (7.22) можно определить по формулам.

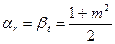, (7.23)

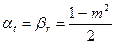, (7.24)

m= 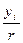, r- наружный радиус диска ;

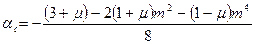, (7.25)

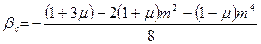. (7.26)

Расчет конического диска производиться по таким же формулам, что и диска постоянной толщины.

Литература.

1. Абианц В.Х. Теория авиационных газовых турбин. – М. : Машиностроение,1979. – 246 с.

2. Биржаков М.Б., Литинецкий В.В. Радиально – осевые ступени мощных турбин. – Л. : Машиностроение (Ленинградское отделение), 1983. – 219с.

3. Жирицкий Г.С., Локай В.И., Макоутова М.К., Струмкин В.А. Газовые турбины двигателей летательных аппаратов. – М.: Машиностроение, 1971.- 620с.

4. Жирицкий Г.С., Стрункин В.А. Конструкция и расчет на прочность деталей паровых и газовых турбин. – М.: Машиностроение, 1968.- 520с.

5. Зайцев В.И., Грицай Л.Л., Моисеев А.А. Судовые паровые и газовые турбины. – М. : Транспорт,1981 –312с.

6. Зайцев Ю.И.Основы проектирования судовых паровых турбоагрегатов. – Л: Судостроение,1974 –439с.

7. Конюков В.Л. Теория турбинной ступени. Конспект лекций.

8. Курзон А.Г. Теория судовых паровых и газовых турбин. – Л. : судостроение, 1970. – 592 с.

9. Маслов Л.А. судовые газотурбинные установки – Л.: Судостроение, 1973 – 400 с.

10. Моисеев А.А., Розенборг А.Н. Конструктирование и расчет прочности судовых ТЗА.- Л.: Судостроение, 1964. – 510 с.

11. Щегляев А.В. паровые турбины. –М: Энергия, 1976, - 366с.

© доцент, к.т.н., зав. кафедрой СЭУ КГМТУ Конюков В.Л.

СПЕЦИАЛЬНЫЕ ВОПРОСЫ СУДОВЫХ ТУРБОМАШИН

Конспект лекций

по дисциплине «Судовые турбинные установки и их эксплуатация» (3 часть)

для студентов 3, 4 курса дневной формы обучения и студентов 4,5 курса

заочной формы обучения направления 6.070104 специальности

«Эксплуатация судовых энергетических установок»

Подписано в печать ________ Объём 1,4 п.л.

Тираж ________экз. Заказ №_____

Издательство: «Керченский государственный морской технологический университет».

г. Керчь, ул. Орджоникидзе, 82.