Визначення мультиколінеарності.
Тест 1. Велике значення коефіцієнта множинної детермінації 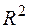 й одночасно незначимість великої кількості параметрів моделі. Так, якщо для моделі
й одночасно незначимість великої кількості параметрів моделі. Так, якщо для моделі 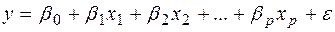 коефіцієнт множинної детермінації близький до одиниці (
коефіцієнт множинної детермінації близький до одиниці ( 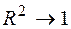 ), а гіпотезу про незначимості параметрів моделі
), а гіпотезу про незначимості параметрів моделі 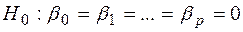 приймаємо.
приймаємо.
Тест 2.Близьке до одиниці значення парних коефіцієнтів кореляції  . Однак навіть при малих
. Однак навіть при малих 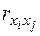 між
між 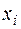 і
і 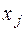 може існувати криволінійна кореляційна залежність.
може існувати криволінійна кореляційна залежність.
Тест 3.Побудова допоміжних регресій.
Необхідно побудувати для кожного фактору регресійну модель залежності від інших факторів, потім розрахувати значення відповідних коефіцієнтів множинної кореляції й перевірити їхня значимість. Якщо хоча б один з побудованих коефіцієнтів кореляції значимо, значить є присутнім мультиколінеарність.
Тест 4.Побудувати для кожного фактору регресійну модель залежності від інших факторів і розрахувати значення відповідних коефіцієнтів множинної детермінації 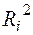
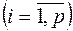 . Розрахувати величину
. Розрахувати величину 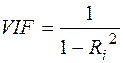 . Якщо
. Якщо 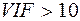 , то є присутнім мультиколінеарність.
, то є присутнім мультиколінеарність.
Тест 5 (за критерієм Пірсона ( 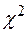 - критерій)). Знаходимо
- критерій)). Знаходимо 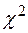 - статистику
- статистику
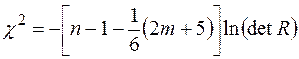 ,
,
де 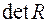 - визначник кореляційної матриці
- визначник кореляційної матриці 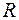 ;
;
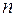 - число спостережень;
- число спостережень;
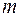 - число факторів
- число факторів
Якщо 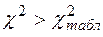 , то існує мультиколінеарність, де
, то існує мультиколінеарність, де 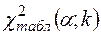 знаходять по таблиці критичних крапок при рівні значимості
знаходять по таблиці критичних крапок при рівні значимості 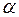 й
й 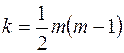 .
.
Тест 6 (за критерієм Фішера ( 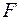 -критерій)).
-критерій)). 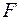 -статистики для кожної пари факторів
-статистики для кожної пари факторів 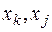 має вигляд
має вигляд
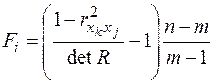 ,
,
де 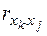 - парні коефіцієнти кореляції.
- парні коефіцієнти кореляції.
Табличне значення 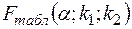 знаходимо по таблиці критичних крапок
знаходимо по таблиці критичних крапок 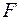 Фішера-Снедекора при
Фішера-Снедекора при 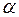 й ступенях волі
й ступенях волі 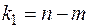 й
й 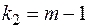 . Якщо
. Якщо 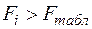 , то змінна
, то змінна 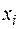 корелює іншими, тобто є присутнім мультиколлинеарность.
корелює іншими, тобто є присутнім мультиколлинеарность.
Тїсть 7 (за критерієм Стьюдента). Для кожної пари факторів знаходимо 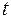 -статистики
-статистики
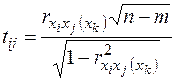 ,
,
де 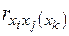 - приватні коефіцієнти кореляції.
- приватні коефіцієнти кореляції.
По таблиці критичних точок 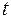 Стьюдента при рівні значимості
Стьюдента при рівні значимості 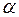 й ступеня волі
й ступеня волі 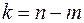 знаходимо
знаходимо 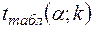 . Якщо
. Якщо 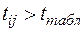 , то між змінними
, то між змінними 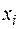 і
і 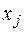 є присутнім мультиколінеарність.
є присутнім мультиколінеарність.
Побудова регресійної моделі в умовах мультиколінеарності
Cпособ 1.Виключення одного з факторів, що корелюють
Нехай фактори 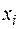 й
й 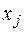 корелюють. Знаходимо парні коефіцієнти кореляції
корелюють. Знаходимо парні коефіцієнти кореляції 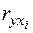 і
і 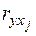 . Якщо
. Якщо 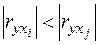 , то виключаємо з розгляду фактор
, то виключаємо з розгляду фактор 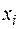 . Після чого параметри моделі визначаємо по методу найменших квадратів.
. Після чого параметри моделі визначаємо по методу найменших квадратів.
Спосіб 2. Побудова фіктивного фактору.
Нехай фактори 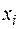 й
й 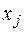 корелюють. Водимо фіктивний фактор
корелюють. Водимо фіктивний фактор 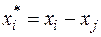 і будуємо регресійну модель у вигляді
і будуємо регресійну модель у вигляді
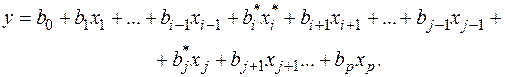
Параметри моделі визначаємо по методу найменших квадратів.
Шляхом найпростіших перетворень переходимо до моделі, що містить вихідний фактор 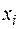
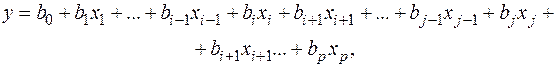
де 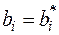 ,
, 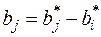 .
.
Дата добавления: 2015-08-14; просмотров: 989;
