Усунення гетероскедастичности

Для усунення гетероскедастичности застосовується узагальнений метод найменших квадратів (ОМНК).

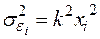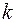1. Якщо гетероскедастичность має вигляд , де - коефіцієнт пропорційності, то необхідно розділити кожний член рівняння регресії на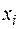

.

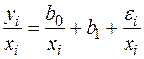Потім, застосовуючи МНК, розрахувати параметри трансформованої моделі.

2. Якщо гетероскедастичность має вигляд 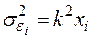, то модель трансформується в такий спосіб

.

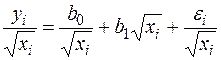3. Якщо гетероскедастичность має вигляд 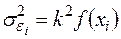, то модель трансформується в такий спосіб:

.

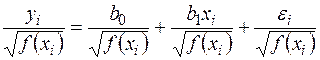Гетерокседастичность проявляється, коли дисперсія випадкової помилки 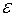не постійна

.

Т. е. значення дисперсії 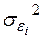залежить від змінної .

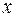Існують різні види гетерокседастичности (форми зв'язку між 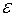і ).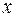

Можливі також випадки убування 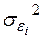й ін.

Гетерокседастичность спостерігається в економічних процесах, коли невраховані фактори (які й впливають на величину 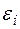) мають тенденцію, наприклад, до росту при збільшенні .

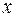Наприклад, при дослідженні залежності між

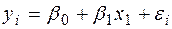
де 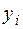– заощадження 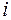-ой родини;

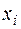– дохід 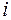-ой родини.

У цьому випадку може спостерігатися гетерокседастичность, тому що родини з більшим доходом ( 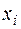більше) показують більшу варіацію у своєму поводженні заощаджень ( 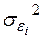більше). Родини з високим доходом схильні дотримуватися певних стандартів життя, і якщо їхній дохід падає, вони скоріше схильні скоротити свої заощадження, чим споживання. З іншого боку, родини з низьким доходом відкладають заощадження з певною метою й тому їхнього заощадження більше регулярні.

Або інший приклад: залежність кількості помилок 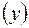під час диктанту від кількості годин 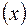, відведених на практику. Зі збільшенням 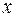(практики) 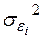зменшується (менше помилок).

Аналогічно, компанії з більшими прибутками 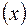ведуть більше ризиковану політику девидентов і тому 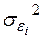в них більше, ніж у малих компаній.