Распределительной (транспортной) задачи

Практически все задачи линейного программирования можно решить, используя ту или иную модификацию симплексного метода. Однако существуют более эффективные вычислительные процедуры решения некоторых типов задач линейного программирования, основанные на специфике ограничений этих задач. Рассмотрим так называемую транспортную задачу по критерию стоимости, которую можно сформулировать следующим образом.

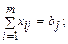
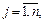(1)

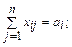
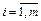, (2)

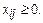
В т пунктах отправления А₁, А₂,...,А_т,, которые в дальнейшем будем называть поставщиками, находится а_i (i = 1, 2, ..., т) единиц некоторого однородного продукта.Данный продукт потребляется в п пунктах В₁, В₂,…, В_n, которые будем называть потребителями; объем потребления обозначим b_j (j = 1, 2, ..., п). Известны расходы на перевозку единицы продукта из пункта A_i в пункт B_j, которые равны c_ij и приведены в матрице транспортных расходов С = (с_ij).

Требуется составить такой план прикрепления потребителей к поставщикам, т.е. план перевозок, при котором весь продукт вывозится из пунктов A_i в пункты B_j в соответствии с потребностью и общая величина транспортных издержек будет минимальной.

Обозначим количество продукта, перевозимого из пункта A_i в пункт B_j, через x_ij. Совокупность всех переменных x_ij для краткости обозначим 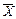, тогда целевая функция задачи представляет собой линейную форму:

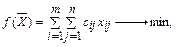(3)

Условия (1) означают полное удовлетворение спроса во всех пунктах потребления; условия (2) определяют полный вывоз продукции от всех поставщиков.

Необходимым и достаточным условием разрешимости задачи (1) – (3) является условие баланса:

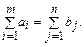(4)