Решение транспортной задачи. Имеется 3 поставщика и 3 потребителя
Имеется 3 поставщика и 3 потребителя. Ресурсы 1-го поставщика составляют 10 ед. , 2-го – 8, 3-го – 13. Потребности потребителя А составляют 6 ед., Б – 14 ед., В – 11 ед. Транспортная задача закрытая.
Издержки на транспортировку единицы груза с учетом расстояния между поставщиками и потребителями приведены в таблице 10.
Таблица 10 - Издержки на транспортировку единицы груза
от поставщиков к потребителю
| Поставщики | Потребители | ||
| А | Б | В | |
Необходимо найти такой вариант грузоперевозок, чтобы суммарные издержки были минимальными.
Сформируем задачу линейного программирования:
Х11 – объем перевозки грузов от 1-го поставщика в потребителю А,
…
Хij – объем перевозки груза от i-го поставщика к потребителю j,
…
Х33 – объем перевозки от 3-го поставщика к потребителю В.
Ограничения по объемам поставки:
1-го поставщика: Х11 + Х12 + Х13 = 10
2-го поставщика: Х 21 + Х22 + Х23 = 8
3-го поставщика: Х31 + Х32 + Х33 = 13
Ограничения по потребностям:
Потребителя А: Х11 + Х21 + Х31 = 6
Потребителя Б: Х12 + Х22 + Х32 = 8
Потребителя В: Х13 + Х23 + Х33 = 13
Целевая функция:
С (min) = 4 Х11 + 5Х12 + 4Х13 + 2Х21 + 3Х22 + 6Х23 + Х31 + 2Х32 + 4Х33
Данная задача отвечает всем требованиям линейного программирования. Ее можно решить симплексным методом. Однако, учитывая, что она имеет особую, довольно простую структуру, ее решают более простым распределительным методом.
Первоначальный план составляют различными методами. Наиболее простой из них метод северо-западного угла.
Алгоритм метода северо-западного угла
1.Выбирается левая верхняя клетка таблицы.
2.В эту клетку записывается базисная переменная:
a)Сравниваем ресурсы (а1) и потребности (b1).
Если а1>b1, то Х11 = b1 и клетка объявляется базисной. В клетку записывается Х11.
Подсчитывается новый ресурс: 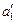 =а1–b1 из таблицы исключается первый столбец.
Делается переход к п. 1 для новой таблицы (без исключенного столбца).
b)Если а1<b1, то Х11 = а1. Подсчитывается новая потребность =а1–b1 из таблицы исключается первый столбец.
Делается переход к п. 1 для новой таблицы (без исключенного столбца).
b)Если а1<b1, то Х11 = а1. Подсчитывается новая потребность  =b1 – а1. Из таблицы исключается первая строка.
Переход к п. 1 для новой таблицы (без исключенной строки).
c)Если а1 = b1, то Х11 = а1 = b1. Подсчитывается =b1 – а1. Из таблицы исключается первая строка.
Переход к п. 1 для новой таблицы (без исключенной строки).
c)Если а1 = b1, то Х11 = а1 = b1. Подсчитывается 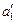 = 0 (или = 0 (или  =0). Из таблицы исключается столбец или строка (условно можно принять исключение строки).
Переход к п. 1 новой таблицы (без строки). =0). Из таблицы исключается столбец или строка (условно можно принять исключение строки).
Переход к п. 1 новой таблицы (без строки).
|
Использование метода северо-западного угла позволило получить первоначальный план перевозки грузов (табл. 11).
Таблица 11 - Первоначальный план перевозки грузов
по методу северо-западного угла
| Поставщики | Потребители | ui | |||
| А | Б | В | |||
| 6 х | 14 10 2 х | 11х | |||
| 10 4 х | 4) | 5) | |||
| 8 х | 3) | -2 | |||
| 13 11 х | 2) | 4) | -3 | ||
| vj |
Клетки 1–А, 1-Б, 2-Б, 3-Б, 3-В занятые, остальные – свободные.
С1 = 4 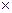 6 + 5
6 + 5 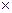 4 + 3
4 + 3 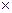 8 + 2
8 + 2 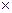 2 +4
2 +4 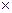 11=116
11=116
Более эффективным методом построения первоначального варианта решения транспортной задачи является метод минимального элемента в таблице. Отличие его от метода северо-западного угла состоит в том, что начинают заполнять таблицу с клетки, в которой находится минимальное значение коэффициента целевой функции, для которой тоже сравниваются объемы поставки и потребности, записывается минимальное их значение и из таблицы исключается строка или столбец. Далее в оставшейся части таблицы отыскивается следующая клетка с минимальными транспортными затратами и осуществляются указанные действия до заполнения всей таблицы. Результаты использования метода минимального элемента приведены в таблице 12.
Таблица 12 – Первоначальное решение транспортной задачи,
построенное методом минимального элемента
в таблице
| Поставщики | Потребители | ui | |||
| А | Б | В | |||
| 6х | 147 х | 111 х | |||
| 10 х | 4) | ||||
| 8 1 х | 3)
  + 7 + 7
| 6)
 - 1 - 1
| |||
| 137 х | 1) | 2) -
 7 7
| 4 + | ||
| vj |
Клетка 1-В, 2-Б, 2-В, 3-А, 3-Б – занятые (базисные), остальные – свободные (небазисные).
С1=4 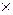 10+3
10+3 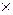 7+6
7+6 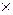 1+1
1+1 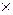 6+2
6+2 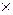 7=87
7=87
Значение целевой функции в этом варианте на 29 руб. меньше, чем в случае использования метода северо-западного угла.
Необходимо проверить, является ли данный план оптимальным? Если план не оптимален, то его следует улучшить.
Оптимальность плана устанавливают при помощи метода потенциалов. Этот метод позволяет также улучшить план.
Алгоритм метода потенциалов
0)Записывается исходное опорное решение.
1)Определяются потенциалы строчек (ui) и столбцов (vj). Обычно u1=0. Остальные рассчитываются по формуле:
cij = ui + vj,
где cij – издержки на перевозку единицы груза в занятых клетках.
2)Вычисляются характеристики свободных клеток:
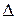 ij = cij – (vj + ui)
3)Если все характеристики неотрицательны, то при решении задачи на минимум получено оптимальное решение. Если же имеется хотя бы одна отрицательная оценка, то это обозначает, что составленный план не оптимален и его можно улучшить.
4)Выбирается наименьшая характеристика. По контуру свободной клетки с этой характеристикой производится преобразование однократного замещения (ПОЗ).
Осуществляется переход к п. 1. ij = cij – (vj + ui)
3)Если все характеристики неотрицательны, то при решении задачи на минимум получено оптимальное решение. Если же имеется хотя бы одна отрицательная оценка, то это обозначает, что составленный план не оптимален и его можно улучшить.
4)Выбирается наименьшая характеристика. По контуру свободной клетки с этой характеристикой производится преобразование однократного замещения (ПОЗ).
Осуществляется переход к п. 1.
|

Характеристики указывают на величину экономии (по сравнению с составленным планом), которую можно получить при улучшении плана, связанного с введением в клетку (i,j) единицы перевозки груза.
Клетку 3-В следует ввести в базис. Для нее необходимо провести ПОЗ.
Построим для нее замкнутый прямоугольный контур.
| Правила построения контура 1. Одна вершина контура должна лежать в свободной клетке, а остальные – в занятых клетках. 2. Звенья контура должны располагаться только по строкам и столбцам таблицы. Для каждой свободной клетки можно построить единственный контур. Число вершин всегда четное. 3. Вершины контура размечают чередующимися знаками «+» и «-», начиная с той вершины, которая лежит в свободной клетке. Этой вершине присваивают знак «+». |
Далее производится улучшение плана.
| Алгоритм улучшения плана (ПОЗ): 1. Из всех вершин прямоугольного контура, помеченных знаком «-», выбирают ту, в которой записан минимальный объем грузоперевозок. 2. Этот объем грузоперевозок последовательно вычитают из всех объемов, расположенных в отрицательные вершинах контура, и прибавляют ко всем объемам грузов в положительных вершинах контура. |
В результате выполнения указанного алгоритма клетка с минимальным объемом груза становится свободной, т. е. выводится из базиса, а выбранная клетка – заполненной, т. е. вводится в базис (табл. 13).
Таблица 13 - Вторая таблица транспортной задачи
| Поставщики | Потребители | ui | ||||
| А | Б | В | ||||
| 4) | ||||||
  + +
| 3)
 - 8 - 8
| |||||
1)
 - 6 - 6
| 2) + 6 | 4) | ||||
| vj | ||||||
С2 = 4×10 + 3×8 + 1×6+2×6 + 4× 1 = 86
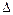 11=4 – (1+0)=3
11=4 – (1+0)=3 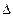 21 = 2 – (1 + 1) = 0
21 = 2 – (1 + 1) = 0
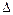 12 = 5 – (0 + 2) = 3
12 = 5 – (0 + 2) = 3 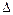 23 = 6 – (1 + 4) = 1
23 = 6 – (1 + 4) = 1
Решение оптимально, поскольку все оценки неотрицательны. Поскольку имеется нулевая оценка ( 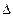 21=0), то имеется еще одно альтернативное оптимальное решение. Для его нахождения в базис вводят клетку с нулевой оценкой (табл. 14).
21=0), то имеется еще одно альтернативное оптимальное решение. Для его нахождения в базис вводят клетку с нулевой оценкой (табл. 14).
Таблица 14 – Таблица транспортной задачи с альтернативным
оптимальным решением
| Поставщики | Потребители | ui | |||
| А | Б | В | |||
| 4) | |||||
| 2) | 3) | ||||
| 2) | 4) | ||||
| vj |
С4 = 4×10 + 2×6 + 3×2 + 2×12 + 4×1 = 86
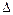 11 = 4 – (1 + 0) = 3
11 = 4 – (1 + 0) = 3 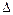 12 = 5 – (2 + 0) = 3
12 = 5 – (2 + 0) = 3
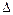 31 = 1 – (1 + 0) = 0
31 = 1 – (1 + 0) = 0 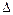 23 = 6 – (4 + 1) = 1
23 = 6 – (4 + 1) = 1
От этого оптимального решение можно снова вернуться к предыдущему.
Дата добавления: 2015-08-14; просмотров: 2616;
