Лекция 6. МЕТОДЫ ТЕОРИИ ИГР

1. Основные понятия теории игр

2. Матричные игры

3. Критерии оптимизации в играх с природой. Принятие решений
в условиях неопределенности

Основные понятия теории игр

На предприятиях теория игр может применяться для выбора оптимальных решений, например, при создании рациональных запасов сырья, материалов, полуфабрикатов, когда противоборствуют две тенденции: увеличение запасов, гарантирующих бесперебойную работу производства, и сокращения запасов в целях минимизации. В сельском хозяйстве теория игр может применяться при решении таких экономических задач, как выбор для посева одной из возможных культур, урожай которых зависит от погоды, если известны цена единицы той или иной культуры и средняя урожайность каждой культуры в зависимости от погоды (например, будет ли лето засушливым, нормальным или дождливым); в этом случае одним из игроков выступает сельскохозяйственное предприятие, стремящееся обеспечить наибольший доход, а другим – природа.

Решение подобных задач требует полной определенности в формулировании их условий (правил игры); установления количества игроков, выявления возможных стратегий игроков, возможных выигрышей (проигрыш понимается как отрицательный выигрыш). Важным элементом в условии игровых задач является стратегия, т.е. совокупность правил, которые в зависимости от ситуации в игре определяют однозначный выбор действий данного игрока. Если в процессе игры игрок применяет попеременно несколько стратегий, то такая стратегия называется смешанной, а ее элементы – чистыми стратегиями. Количество стратегий у каждого игрока может быть конечным и бесконечным, в зависимости от этого игры подразделяются на конечные и бесконечные.

Важными являются понятия оптимальной стратегии, цены игры, среднего выигрыша. Эти понятия находят отражения в определении решения игры: стратегии Р* и Q* первого и второго игрока соответственно называются их оптимальными стратегиями, а число V – ценой игры, если для любых стратегий P первого игрока и любых стратегий Q второго игрока выполняются неравенства:

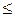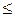M (P,Q*) V M (P*,Q), (1)

Где M (P,Q) означает средний выигрыш первого игрока, если первым и вторым игроками избраны соответственно стратегии P и Q.

Из неравенства (1) следует, в частности, что V=M(P*,Q*), т.е. цена игры равна среднему выигрышу первого игрока, если оба игрока изберут оптимальные для себя стратегии.