Матричные игры
Одним из основных видов игр являются матричные игры, которыми называются парные игры с нулевой суммой (один игрок выигрывает столько, сколько проигрывает другой) при условии, что каждый игрок имеет конечное число стратегий. В этом случае парная игра формально задается матрицей А=(aij), элементы которой aij определяют выигрыш первого игрока (и соответственно проигрыш второго), если первый игрок выберет i-ю стратегию ( 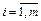 ), а второй – j-ю (
), а второй – j-ю ( 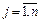 ). Матрица А называется матрицей выигрышей или платежной матрицей.
). Матрица А называется матрицей выигрышей или платежной матрицей.
Рассмотрим построение платежной матрицы на примере.
Пример 1. Сельскохозяйственное предприятие может возделывать n видов зерновых культур. На конкретном поле может возделываться только одна из этих культур. Если зерно вида j ( 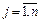 ) будет пользоваться спросом, то предприятие от его реализации получит прибыль Pj. Если же этот вид зерна не будет пользоваться спросом, то издержки на его хранение принесут предприятию убыток gj. Требуется выбрать зерновую культуру, которую целесообразно возделывать на конкретном поле.
) будет пользоваться спросом, то предприятие от его реализации получит прибыль Pj. Если же этот вид зерна не будет пользоваться спросом, то издержки на его хранение принесут предприятию убыток gj. Требуется выбрать зерновую культуру, которую целесообразно возделывать на конкретном поле.
В условиях неопределенного покупательского спроса конфликтная ситуация производства продукции формализуется матричной игрой. Пусть первый игрок – предприятие, второй игрок – покупательский спрос. Каждый из игроков имеет по n стратегий. Возделывание i-ой культуры – i-я стратегия первого игрока, спрос на j-й вид зерна – j-я стратегия второго игрока. Тогда матрица выигрышей первого игрока имеет вид квадратной матрицы n-го порядка:
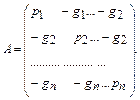
Существует ряд методов решения матричных игр. Если матрица игры имеет одну из размерностей, равную двум (у одного из игроков имеется только две стратегии), то решение игры может быть получено графически. Известно несколько методов приближенного решения матричной игры, - например, метод Брауна.
В качестве примера рассмотрим решение игры, когда матрица имеет так называемую седловую точку.
Пример 2. Исходные данные приведены в таблице 20.
Таблица 20-Урожайность озимой пшеницы при различных нормах
внесения удобрений и сроках выпадения дождей, ц/га
| Норма внесения удобрений, кг/га | Сроки выпадения дождей | ||||
| при подготовке к почве | перед посевом | ранней весной | в конце мая | ||
| У1 | У2 | У3 | У4 | ||
| Х1 | 27,1 | 28,7 | 30,5 | 31,0 | |
| Х2 | 28,3 | 28,5 | 28,6 | 29,0 | |
| Х3 | 29,6 | 29,9 | 31,7 | 33,0 | |
| Х4 | 31,0 | 32,0 | 31,2 | 31,7 |
Требуется определить, какие нормы удобрения следует вносить на 1 га посевов озимой пшеницы в зависимости от срока выпадения дождей, чтобы получить максимальную урожайность.
Чистые стратегии хозяйства – внесение различных доз, обозначим через Хi. Чистые стратегии погоды – сроки выпадения дождей, обозначим через Yj. Хозяйство и погода имеют по четыре чистых стратегии.
Проанализируем их возможные действия. Если бы хозяйству было известно, в какие периоды выпадает дождь, то оно могло бы в каждой ситуации выбрать наилучшую стратегию. Если погода примет одну из своих стратегий, тогда наилучшими ходами хозяйства будут:
Срок выпадения дождей Y1 Y2 Y3 Y4
 |
Норма внесения удобрений X1 X2 X3 X4
 |  | |||||||||
 | ||||||||||
 |  |  | ||||||||
 | ||||||||||
Урожайность (ц/га) 31 32 31,7 33
Однако хозяйство наперед не знает, какая будет погода. Какую же стратегию выбрать в качестве наиболее выгодной?
Выбирая какую-либо стратегию Хi из 4-х возможных, хозяйство поступит рационально, если будет рассчитывать на то, что погода будет наименее благоприятной:
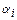 =
= 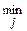 aij
aij
Из платежной матрицы игры видно, что наименьший выигрыш, который может получить хозяйство при выборе любой из 4-х стратегий, равен: 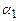 = 27,1,
= 27,1,  = 28,3,
= 28,3, 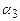 = 29,6,
= 29,6, 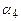 = 31. Эти числа являются наименьшим выигрышем и называются гарантированным выигрышем (уровнем урожайности). Если погода будет даже самой неблагоприятной, то в этих условиях минимум урожайности будет гарантирован.
= 31. Эти числа являются наименьшим выигрышем и называются гарантированным выигрышем (уровнем урожайности). Если погода будет даже самой неблагоприятной, то в этих условиях минимум урожайности будет гарантирован.
Но хозяйство может выбрать ту из стратегий Хi, для которых число 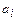 является максимальным:
является максимальным:
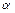 =
= 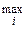
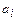 =
= 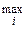 (
( 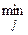 aij).
aij).
Величина 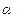 называется максимальным выигрышем среди минимальных уровней урожайности или максимином. Стратегия, которая находится в соответствующей строке платежной таблицы, называется максимином. Максимин
называется максимальным выигрышем среди минимальных уровней урожайности или максимином. Стратегия, которая находится в соответствующей строке платежной таблицы, называется максимином. Максимин 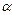 = 31.
= 31.
Это гарантийная урожайность, которую может получить хозяйство, придерживаясь наиболее эффективной стратегии. Величина 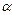 называется нижней ценой игры.
называется нижней ценой игры.
Аналогичные рассуждения можно вести с позиции природы. Гарантированные урожаи для хозяйства будут рассматриваться как наибольшие проигрыши природы.
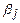 =
= 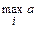 ij ,
ij ,
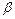 =
= 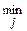
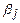 =
= 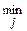 (
( 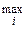 aij)
aij)
Наибольшие проигрыши, или гарантированные природные уровни урожайности, равны: 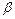 1 = 31,
1 = 31, 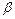 2 = 32,
2 = 32, 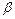 3 = 31,7,
3 = 31,7, 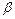 4 = 33.
4 = 33.
Минимальный гарантированный уровень, или наименьший среди наибольших проигрышей, равный 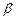 = 31, называется минимаксом или верхней ценой игры.
= 31, называется минимаксом или верхней ценой игры.
Если нижняя и верхняя цены игры совпадают, то их общее значение называется чистой ценой игры и обозначается 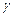 . Эта точка равновесия, или седловая точка платежной матрицы.
. Эта точка равновесия, или седловая точка платежной матрицы.
Стратегии Х4 для хозяйства и У1 для природы называются оптимальными чистыми стратегиями, а их нахождение – оптимальным решением задачи.
3. Критерии оптимизации в играх с природой.
Принятие решений в условиях неопределенности
Во многих игровых задачах в сфере экономики неопределенность вызвана не сознательным противодействием противника, а недостаточной осведомленностью об условиях, в которых действуют стороны. Так, в рассматриваемых выше примерах были неизвестны заранее погода в некотором регионе, покупательский спрос на некоторую продукцию.
Подобного рода игры называются играми с природой. В этих случаях строки матрицы игры соответствуют стратегии игрока, а столбцы – состояниям «природы». В ряде случаев при решении такой игры рассматривают матрицу рисков.
При решении игр с природой используется также ряд критериев: критерий Сэвиджа, критерий Вальда, критерий Гурвица и др.
При максиминном критерии Вальда оптимальной считается та стратегия лица, принимающего решение (ЛПР), которая обеспечивает максимум минимального выигрыша; применяя этот критерий, ЛПР в большей степени ориентируется на наихудшие условия (этот критерий иногда называют критерием «крайнего пессимизма»).
Критерий минимаксного риска Сэвиджа предполагает, что оптимальной является та стратегия, при которой величина риска в наихудшем случае минимальна.
При использовании критерия «пессимизм - оптимизм» Гурвица ЛПР выбирает некоторый так называемый «коэффициент пессимизма» g; при g=1 критерий Гурвица приводит к критерию Вальда («крайнего пессимизма»), а при g=0 – к критерию «крайнего оптимизма».
Рассмотрим пример использования указанных критериев в играх с природой.
Пример 3.Диспетчер хозяйства (ЛПР) во время уборки должен принять решение о целесообразности заказа дополнительных автомобилей на перевозку урожая. ЛПР имеет три варианта решений: увеличить количество автомобилей на 10 (стратегия Р1), увеличить это количество на 5 (стратегия Р2) или оставить без изменения обычное число автомобилей (стратегия Р3). Возможны два состояния погоды: Q1 – плохая погода, Q2 – хорошая погода, причем в момент принятия решения нет возможности определить ожидаемое состояние погоды. Если в ближайшие дни будет хорошая погода и будет убрано больше зерновых культур, а выделено мало автомобилей, то хозяйство понесет убытки, связанные с простоем комбайнов. Если же выделены дополнительные автомобили, а погода окажется плохой, то возникнут потери вследствие простоя автомобилей.
Пусть на основе анализа статистических данных за определенный период установлена функция потерь для возможных комбинаций состояний природы и решений ЛПР в виде матрицы игры A(Pi, Qj), в которой отрицательные значения показывают убытки, а положительные – потери:
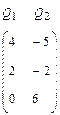
Р1
А= Р2
Р3
Если нет сведений о вероятностях различных состояний погоды, то по критерию Вальда и по критерию Сэвиджа оптимальной является стратегия Р2. По критерию Гурвица при «коэффициенте пессимизма» g=1 оптимальной окажется стратегия Р2, а при g=0 – стратегия Р1.
Рассмотрим в заключение конкретный числовой пример решения задачи принятия решения в экономике методами теории игр.
Пример 4.Швейное предприятие, выпускающее детские платья и костюмы, реализует свою продукцию через фирменный магазин. Сбыт продукции зависит от состояния погоды. По данным прошлых наблюдений предприятие в течение апреля – мая в условиях теплой погоды может реализовать 600 костюмов и 1975 платьев, а при прохладной погоде – 1000 костюмов и 625 платьев. Известно, что затраты на единицу продукции в течение указанных месяцев составили для костюмов 27 руб., для платьев 8 руб., а цена реализации равна соответственно 48 руб. и 16 руб. (цифры условные).
Задача заключается в максимизации средней величины прибыли от реализации выпущенной продукции с учетом неопределенности погоды в рассматриваемые месяцы. Таким образом, служба маркетинга предприятия должна в этих условиях определить оптимальную стратегию предприятия, обеспечивающую при любой погоде определенный средний доход. Решим эту задачу методами теории игр, игра в этом случае будет относиться к типу игр с природой.
Предприятие располагает в этих условиях двумя чистыми стратегиями: стратегия А – в расчете на теплую погоду и стратегия Б – в расчете на холодную погоду. Природу будем рассматривать как второго игрока, так же с двумя стратегиями: прохладная погода (стратегия В) и теплая погода (стратегия Г). Если предприятие выберет стратегию А, то в случае прохладной погоды (стратегия природы В) доход составит 600 (48 - 27) + 625 (16-8) – (1975 - 625) 8 = 6800 руб., а в случае теплой погоды (стратегия природы Г) доход будет равен 600 (48 - 27) + 1975 (16-8) = 28400 руб.
Если предприятие выберет стратегию Б, то реализация продукции в условиях прохладной погоды даст доход 6100 (48 - 27) + 625 (16-8) = 26000 руб., а в условиях теплой погоды 600 (48 - 27) + 625 (16-8) – (1000 - 600) 27 = 6800 руб.
Следовательно, матрица данной игры (платежная матрица) имеет вид:
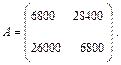
Первая и вторая строки этой матрицы соответствуют стратегиям А и Б предприятия, а первый и второй столбцы – стратегиям В и Г природы.
По платежной матрице видно, что первый игрок (предприятие) никогда не получит доход меньше 6800 руб. Но если погодные условия совпадают с выбранной стратегией, то выручка (выигрыш) составит 26000 или 28400 руб. Отсюда можно сделать вывод, что в случаях неопределенности погоды наибольший гарантированный доход предприятие обеспечит, если будет попеременно применять то стратегию А, то стратегию Б. Такая стратегия, как отмечалось выше, называется смешанной. Оптимизация смешанной стратегии позволит первому игроку всегда получать среднее значение выигрыша независимо от стратегии второго игрока.
Пусть х означает частоту применения первым игроком стратегии А, тогда частота применения им стратегии Б равна (1 - х). В случае оптимальной смешанной стратегии первый игрок (предприятие) получит и при стратегии В (холодная погода), и при стратегии Г (теплая погода) второго игрока одинаковый средний доход: 6800х + 26000 (1-х)=28400х + 6800 (1-х).
Отсюда можно найти, что х=8/17; 1-х=9/17.
Следовательно, первый игрок, применяя чистые стратегии А и Б в соотношении 8:9, будет иметь оптимальную смешанную стратегию, обеспечивающую ему в любом случае средний доход в сумме 6800 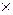 8/17+26000
8/17+26000 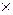 9/17=16965 руб.; эта величина и будет в данном случае ценой игры.
9/17=16965 руб.; эта величина и будет в данном случае ценой игры.
Легко рассчитать, какое количество костюмов и платьев должно выпускать предприятие при оптимальной стратегии: (600 костюмов + 1975 платьев) 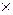 8/17 + (1000 костюмов + 625 платьев)
8/17 + (1000 костюмов + 625 платьев) 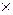 9/17 = 812 костюмов + 1260 платьев.
9/17 = 812 костюмов + 1260 платьев.
Следовательно, оптимальная стратегия предприятия заключается в выпуске 812 костюмов и 1260 платьев, что обеспечит ему при любой погоде средний доход в сумме 16965 руб.
Дата добавления: 2015-08-14; просмотров: 1673;
