Особые случаи решения транспортной задачи
Открытая модель транспортной задачи
На практике часто имеет место случай, когда
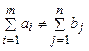
В этом случае транспортная задача называется открытой.
Чтобы решить задачу при таком условии, открытую модель превращают в закрытую. Для этого в условия задачи вводится фиктивный потребитель (или поставщик), спрос которого принимают равным разности между объемом производства и суммой спроса всех действительных потребителей.
Если обозначить спрос фиктивного потребителя через b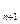 
, то
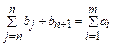
Транспортные издержки по доставке продукции фиктивному потребителю принимают равными 0, поскольку транспортировка фиктивному потребителю осуществляться не будет. Удовлетворение спроса фиктивного потребителя осуществляется в последнюю очередь. Пример открытой транспортной задачи и ее решения приведены в таблицах 15 и 16.
Таблица 15 – Открытая транспортной задачи размещения производства
| Поставщики | Потребители | ui | ||||
| А | Б | В | Фиктивный потребитель | |||
| 450 х | 360 310 150 x | 440 х | 250 х | |||
| 600 160 х |  9) +
 160
| 8) - | ||||
| 400 250 х | 10) -
|  8 +
| 0) 250 | |||
| 500 50 х | 5) | 7) | -2 | |||
| vj | -1 |
С1 = 9×160 + 8×440 + 10×150 +0×250+5×450 + 7×50 = 9060
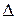11 = 8 – 7 = 1 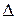14 = 0 + 1 = 1 
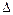21 = 7 – 8 = -1
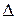23 = 8 – 9 = -1 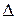33= 11 – 6 = 5 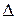34 = 0 + 1 = 1
Таблица 16 – Решение открытой транспортной задачи
| Поставщики | Потребители | ui | ||||
| А | Б | В | Фиктивный потреби- тель | |||
| 9) | 8) | |||||
| 8) | 0) | |||||
| 5) | 7) | -2 | ||||
| vj |
С2 = 8 910
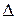11 =8 – 7 = 1 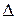14 = 0 – 0 = 0 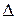21 = 7 – 7 = 0
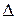33 = 11 – (8 - 2) = 5 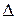34 = 0 + 2 = 2 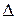22 = 10 – 9 = 1
Важной особенностью транспортной задачи является то, что ее модель позволяет определить минимальные издержки не только на перевозки, но и на производство продукции вместе с доставкой ее потребителю.
Составление открытой модели с применением указанного критерия позволяет оценить перспективы предприятий, производящих однородную продукцию, в случае, если предложение превышает спрос на рынке данной продукции. Связь с фиктивным потребителем укажет на необходимость сокращения производства на предприятии.
В рассмотренной задаче на 2-м предприятии производство должно быть снижено с 400 до 150 единиц.
Вырождение при решении задач распределительным методом
Для задачи, решаемой распределительным методом, в каждой таблице необходимо выполнение следующего правила: количество заполненных клеток должно быть равно k=n+ m – 1. Это правило должно выполняться для того, чтобы на каждом шаге улучшения плана была возможность определить потенциалы и построить контур для ПОЗ.
Если же k<n+ m – 1, то вычислить некоторые потенциалы и построить некоторые контуры по общим правилам будет невозможно. Такой случай называется вырожденным. Пример вырождения приведен в таблице 17.
Таблица 17 – Случай вырождения при решении транспортной задачи
| Поставщики | Потребители | ui | ||||
| А | Б | В | Г | |||
| 50 х | 250 х | 200 х | 300 x | |||
| 400 х | 5) | |||||
| 500 450 200 х | 8) | 9) | 8) | |||
| 300 x | 3) | 6) | -3 | |||
| vj |
В некоторых случаях вырождение можно преодолеть, если составить первоначальный план, используя другую диагональ или используя другой метод.
Если же и этот путь приведет к вырождению, то применяют следующий прием: одну из свободных клеток по строке или по столбцу заполняют условно, вписывая в нее 0 (в рассматриваемом примере это клетка (3,2)). Это итогов не искажает. При построении очередной таблицы эту клетку следует считать заполненной.
Дата добавления: 2015-08-14; просмотров: 1631;