Постановка задачи линейного программирования
В задаче линейного программирования (ЗЛП) требуется найти экстремум (максимум или минимум) линейной целевой функции f( 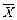 ):
):
max (min) f( 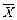 ) = c1x1 + c2x2 + … + cnxn (9)
) = c1x1 + c2x2 + … + cnxn (9)
при ограничениях (условиях):
a11x1 + a12x2 + … + a1nxn { 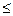 ,=,
,=,  } b1,
} b1,
a21x1 + a22x2 + … + a2nxn { 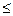 ,=,
,=,  } b2, (10)
} b2, (10)
……………………………………
am1x1 + am2x2 + … + amnxn { 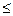 ,=,
,=,  } bm,
} bm,
xj  0, j=
0, j= 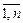 , (11)
, (11)
где аij, bi, cj (i = 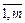 ; j =
; j = 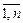 ) – заданные постоянные величины.
) – заданные постоянные величины.
Систему ограничений (10) называют функциональными ограничениями ЗЛП, а ограничения (11) – прямыми.
Вектор 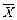 = (x1, x2, …, хn), удовлетворяющий системе ограничений (10), (11), называется допустимым решением, или планом задачи линейного программирования, т.е. ограничения (10), (11) определяют область допустимых решений, или планов задачи линейного программирования (область определения ЗЛП).
= (x1, x2, …, хn), удовлетворяющий системе ограничений (10), (11), называется допустимым решением, или планом задачи линейного программирования, т.е. ограничения (10), (11) определяют область допустимых решений, или планов задачи линейного программирования (область определения ЗЛП).
План (допустимое решение), который доставляет максимум или минимум целевой функции (9), называется оптимальным планом (оптимальным решением) ЗЛП.
Канонической формой записи задачи линейного программирования
(КЗЛП) называют задачу вида (запись с использованием знаков суммирования):
Найти
max f ( 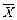 ) =
) = 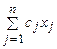 (12)
(12)
при ограничениях
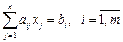 , (13)
, (13)
хj  0, bi
0, bi  0, i=
0, i= 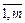 , j=
, j= 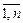 . (14)
. (14)
Векторная форма записи КЗЛП имеет вид:
Найти
max f ( 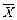 ) =
) = 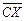
при ограничениях
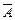 1x1 +
1x1 + 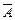 2x2 + … +
2x2 + … + 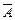 nxn =
nxn = 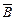 ,
,
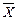
 0,
0,
где 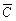 = (с1, с2, … сn),
= (с1, с2, … сn), 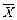 = ( х1, х2,…хn),
= ( х1, х2,…хn),
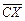 – скалярное произведение векторов
– скалярное произведение векторов 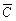 ,
, 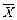 ;
;
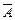 i и
i и 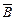 – вектор – столбцы:
– вектор – столбцы:

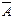 1 =
1 = 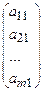 ,
, 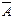 2=
2= 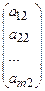 , … ,
, … , 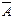 n=
n= 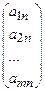 ,
,  =
= 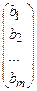 .
.
Матричная форма записи КЗЛП:
max 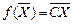
при условиях
А 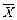 =В,
=В, 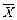
 0
0
Здесь 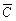 = (c1, с2,..., сп) – вектор-строка; А = (аij) – матрица размерности (m
= (c1, с2,..., сп) – вектор-строка; А = (аij) – матрица размерности (m 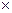 n), столбцами которой являются вектор-столбцы
n), столбцами которой являются вектор-столбцы  j,
j,
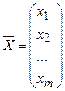 - вектор – столбец,
- вектор – столбец,  - вектор – столбец.
- вектор – столбец.
Приведение ЗЛП к каноническому виду осуществляется введением в левую часть соответствующего ограничения вида (10) k-й дополнительной переменной xn+k со знаком (-) в случае ограничения типа  и знаком (+) в случае ограничения типа
и знаком (+) в случае ограничения типа  .
.
К математическим задачам линейного программирования приводят исследования конкретных производственно-хозяйственных ситуаций, которые в том или ином виде интерпретируются как задачи об оптимальном использовании ограниченных ресурсов (задача о смесях, рационе).
Задача о смесях. Октановое число автомобильного бензина А-76 должно быть не ниже 76, а содержание серы в нем – не более 0,3%. Для производства такого бензина используется четыре компонента. Данные о ресурсах компонентов, их себестоимости, октановом числе и содержании серы приведены в таблице 1.
Таблица 1 – Исходные данные для задачи о смесях
| Характеристика | Компонент автомобильного бензина | |||
| № 1 | № 2 | № 3 | № 4 | |
| Октановое число | ||||
| Содержание серы, % | 0,35 | 0,35 | 0,3 | 0,2 |
| Ресурсы, т | ||||
| Себестоимость, ден.ед./т |
Найти, сколько тонн каждого компонента следует использовать для получения 1000 т автомобильного бензина А-76, чтобы его себестоимость была минимальной.
Решение. Сформулируем экономико-математическую модель задачи. Обозначения: пусть Xj (j = 1,2,3,4) – количество в смеси компонента с номером j. Критерий оптимальности – «минимум себестоимости»:
min f( 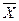 )=40x1+45x2+60x3+90x4,
)=40x1+45x2+60x3+90x4,
x1+x2+x3+x4,=1000, (1а)
68x1+72x2+80x3+90x4,  76
76  1000, (2а)
1000, (2а)
0,35x1+0,35x2+0,3x3+0,2x4,  0,3
0,3  1000, (3а)
1000, (3а)
x1 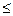 700,
700,
x2 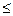 600,
600,
x3 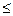 500,
500,
x4 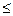 300,
300,
xj  0, j=1,2,3,4.
0, j=1,2,3,4.
Функциональное ограничение (1а) отражает необходимость получения заданного количества смеси (1 000 т), (2а) и (3а) – ограничения по октановому числу и содержанию серы в смеси, остальные – ограничения на имеющиеся объемы соответствующих ресурсов.
Полученная задача относится к линейному программированию. Она решается симплекс-методом. В результате решения получается оптимальное решение.
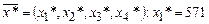 Т,
Т, 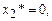

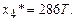
Подставляя найденное решение в целую функцию, находим минимальную себестоимость:
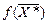 =40
=40 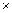 571+45
571+45  0+60
0+60  143+90
143+90  286=57 160,0 (ден. ед.),
286=57 160,0 (ден. ед.),
Использование ограниченных ресурсов.
На строящуюся дорогу необходимо вывезти 20 000 м3 каменных материалов. Имеется три карьера с запасами 8 000 м3, 9 000 м3 и 10 000 м3. Для погрузки материалов используются экскаваторы, имеющие производительность 250 м3 в смену в карьерах 1 и 2 и 500 м3 в смену в карьере 3. На погрузку материалов для экскаваторов выделен общий лимит 60 машино-смен.
Для перевозки 10 000 м3 материалов из карьера 1 требуется 1 000 автомобиле-смен, из карьера 2 – 1 350, из карьера 3 – 1 700 автомобиле-смен. Требуется найти оптимальный план перевозок по критерию минимума транспортных затрат.
Решение. Сформулируем экономико-математическую модель задачи. Примем за единицу измерения количества материалов 10 000 м3.
Пусть х1 - объем добычи материалов в карьере 1, х2 – в карьере 2,
х3 – в карьере 3. Минимизировать транспортные затраты:
min f( 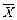 )=1000x1+1350x2+1700x3,
)=1000x1+1350x2+1700x3,
при ограничениях
x1+x2+x3,=2,0; (1а)
40x1+40x2+20x3  60; (2а)
60; (2а)
0  x1
x1  0,8; (3а)
0,8; (3а)
0  x2
x2  0,9; (4а)
0,9; (4а)
0  x3
x3  1,0. (5а)
1,0. (5а)
Условие (1а) отражает потребность в материалах, (2а) – ограничение по балансу ресурса «фонд рабочего времени экскаваторов». Условия (3а)-(5а) отражают ограниченность запасов материалов в соответствующих карьерах. Получена задача ЛП; решение ее симплекс-методом позволит найти оптимальный план:
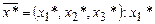 =0,8 (8000 м3)
=0,8 (8000 м3)
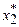 =0,2 (2000 м3);
=0,2 (2000 м3); 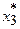 =1,0 (10000 м3).
=1,0 (10000 м3).
Таким образом, из карьера 1 следует вывезти 8 000 м3 материалов, из карьера 2 – 2 000 м3, из карьера 3 – 10 000 м3 при минимальных транспортных затратах
f(X*) = 1 000  0,8 + 1350
0,8 + 1350  0,2 + 1 700
0,2 + 1 700  1,0 = 2 770 (автомобиле-смен).
1,0 = 2 770 (автомобиле-смен).
Экономическая постановка сельскохозяйственной задачи.
Фермерское хозяйство занимается возделыванием только двух культур (зерновых и сахарной свеклы), располагая следующими ресурсами: пашня - 5 га, труд - 300 чел. – дней. Цель производства - получение максимального объема валовой продукции в стоимостном выражении. Требуется найти оптимальное сочетание посевных площадей культур.
Нормы затрат ресурсов и выхода продукции приведены в таблице 2.
Таблица 2 - Нормы затрат и выхода продукции в хозяйстве
| Культура | Затраты ресурсов на 1 га посева | Выход валовой продукции с 1 га, тыс. руб. | |
| труда, чел.-дн. | пашни, га | ||
| Зерновые культуры (х1) | |||
| Сахарная свекла (х2) |
Критерием оптимальности (показателем оценки качества варианта решения) является максимум стоимости валовой продукции. Этот максимум должен достигаться при использовании ограниченных ресурсов пашни и труда. Указанные ресурсы выступают в качестве ограничивающих условий задачи, а показатели, приведенные в таблице 2, являются технико-экономическими коэффициентами (коэффициентами затрат и выпуска продукции). Задача является многовариантной, поскольку имеется множество допустимых вариантов сочетаний посевных площадей двух культур.
Для определения варианта, обеспечивающего экстремальное (в данном случае максимальное) значение целевой функции, пересмотр всех возможных вариантов сочетания площадей неэффективен из-за большой трудоемкости. При реальном достаточно большом числе культур, ресурсов и дополнительных условий расчет всех вариантов практически невозможен.
Исходя из логических рассуждений можно предложить, что всю площадь необходимо занять той культурой, которая обеспечивает наибольший выход валовой продукции с 1 га (в данном случае сахарной свеклой). Но для возделывания 5 га сахарной свеклы потребовалось бы 5  150=750 чел. – дн., что значительно превышает наличные ресурсы труда. Необходимость одновременного учета всех ресурсов еще более усложняет задачу.
150=750 чел. – дн., что значительно превышает наличные ресурсы труда. Необходимость одновременного учета всех ресурсов еще более усложняет задачу.
Для нахождения оптимального варианта решения методами линейного программирования необходимо математически формулировать (описать) условия и ограничения задачи.
Математическая формулировка задачи линейного программирования.
В нашем примере неизвестными величинами являются посевные площади зерновых культур и сахарной свеклы в гектарах (х1 и х2). Критерий оптимальности - стоимость валовой продукции - определяется как сумма произведений стоимости продукции с 1 га на посевные площади (тыс. руб.):
Zmax=4x1+10x2.
Максимум целевой функции должен быть достигнут при соблюдении следующих условий:
1. Общая площадь зерновых культур и сахарной свеклы не должна превышать площади пашни, га:
x1+x2 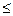 5.
5.
2. Затраты труда не должны быть больше наличных ресурсов (чел. – дн.):
30x1+150x2 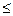 300.
300.
3. Площади не могут быть отрицательными величинами:
х1  0, х2
0, х2 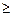 0.
0.
Таким образом, условия задачи выражаются в виде следующей системы неравенств:
x1+x2 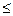 5;
5;
30x1+150x2 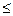 300;
300;
x1  0; x2
0; x2  0.
0.
Целевая функции: Zmax=4x1+10x2.
Приведенные неравенства называют ограничениями экстремальной задачи линейного программирования.Число ограничений в задачах может быть очень большим – от десятков до многих сотен и тысяч.
В целевую функцию и систему ограничений переменные х1 и х2 входят только в первой степени, то есть все математические соотношения являются линейными. Таким образом, рассматриваемый пример относится к задачам линейного программирования.
При формулировке ограничений в задаче не должно быть противоречивых условий. Например, если одновременно ввести условия: площадь зерновых культур не менее 3 га и сахарной свеклы не менее 4 га, то задача станет неразрешимой, так как имеется лишь 5 га пашни.
Дата добавления: 2015-08-14; просмотров: 1157;
