Решение задачи симплексным методом
Рассмотрим алгоритм симплексного метода на примере задачи, которая была решена графическим способом.
Запишем условия задачи в канонической форме:
x1+x2+x3=5;
30x1+150x2+x4=300;
x1  0, x2
0, x2  0, x3
0, x3  0, x4
0, x4  0
0
при целевой функции Zmax = 4x1+10x2+0x3+0x4. Переменные х1 и х2, которые фигурировали в системе до приведения ее в каноническую форму, называют основными переменными задачи. В канонической форме эта система состоит из двух уравнений с четырьмя переменными. Переменные х3 и х4 называются дополнительными. Они обозначают недоиспользование ресурсов (пашни и труда). Такая система, как известно, является неопределенной и имеет бесконечное множество решений.
Рассмотрим решение системы. Вначале выпишем коэффициенты при неизвестных (аij) и свободные члены (bi) в виде матрицы:
 x1 x2 x3 x4 bi
x1 x2 x3 x4 bi
1 1 1 0 5
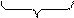 30 150 0 1 300
30 150 0 1 300
Коэффициенты при дополнительных переменных образуют подматрицу, по главной диагонали которой стоят единицы; такую матрицу называют единичной.
Набор k переменных, коэффициенты которых образуют единичную матрицу, называют базисом k-мерного векторного пространства, соответствующие им переменные - базисными переменными, остальные – свободными.
В общем случае, если система в канонической форме содержит n переменных и m уравнений, то n - m = s являются свободными переменными. В рассматриваемом примере две свободные переменные (4-2 = 2). Чтобы решить систему, нужно задать свободным переменным некоторое произвольное значение. Обычно их принимают равными нулю.
В рассматриваемой системе базисными переменными являются х3, х4.. Если свободные переменные х1 и х2 приравнять к нулю, то решением системы будет: х3 = 5; x4 = 300; (при x1 = 0 и х2 = 0). Следовательно, решением системы является матрица-столбец свободных членов, и при этом все переменные неотрицательны (хj  0). Решение, где все переменные неотрицательны, называют допустимым. Такое решение, полученное приравниванием свободных переменных нулю, называют опорным (базисным) решением или опорным планом. Оптимальный вариант плана обязательно находится в числе допустимых решений.
0). Решение, где все переменные неотрицательны, называют допустимым. Такое решение, полученное приравниванием свободных переменных нулю, называют опорным (базисным) решением или опорным планом. Оптимальный вариант плана обязательно находится в числе допустимых решений.
Хотя задача линейного программирования имеет большое количество допустимых решений, число базисных решений ограничено. Это позволяет выбирать оптимальный вариант из сравнительно небольшого числа решений. Опорные решения геометрически соответствуют только вершинам выпуклого многогранника.
Схема поиска оптимального плана строится так: сначала определяют некоторый опорный план (как правило, он оказывается неоптимальным); найденный план проверяется на оптимальность. Если опорный план оказался неоптимальным, вычисляется другой, лучший, который снова проверяется на оптимальность, и т. д. до получения оптимального варианта.
Симплексным методом предусмотрена такая схема расчетов, когда на каждом новом этапе план улучшается. Поэтому он называется также методом последовательного улучшения плана.
Нахождение первого опорного плана. Приступая к решению задачи, в качестве базисных переменных берут дополнительные переменные (х3, х4,) , а в качестве свободных – основные переменные (х1, х2), т.е. те, которые были в системе до приведения ее в каноническую форму. Затем, приравняв нулю свободные переменные х1 = 0 и х2 = 0, получают первое опорное решение. Для этого выразим базисные переменные через ободные – преобразуем исходные уравнения так, чтобы в правой части были только свободные переменные:
х3 = 5 – х1 – х2; х4 = 300 – 30х1 – 150х2 .
Подставляя в уравнения нулевые значения свободных переменных (х1=0 и х2=0), получим первое опорное решение: х3 =5; х4 =300. Полученный вариант плана формально является допустимым (все хj  0), но экономически он неприемлем, так как площади зерновых культур и сахарной свеклы равны нулю, продукция не производится, а целевая функция равна нулю. Равенство дополнительных переменных свободным членам уравнений показывает, что наличные ресурсы не используются.
0), но экономически он неприемлем, так как площади зерновых культур и сахарной свеклы равны нулю, продукция не производится, а целевая функция равна нулю. Равенство дополнительных переменных свободным членам уравнений показывает, что наличные ресурсы не используются.
Экономический смысл дополнительных переменных состоит в следующем. Записывая ограничение по пашне в виде нестрогого неравенства х1+х2 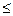 5, допускались следующие два случая: а) вся пашня будет использована, тогда х1+х2=5 (и х3 =0); б) если при сложившихся условиях хозяйству невыгодно использовать всю пашню, т.е. х1+х2<5 (и х3>0), то в этом случае х3 показывает неиспользуемую часть пашни. Переменная х4 отражает неиспользованную часть ресурсов труда. Неиспользуемые ресурсы не могут увеличивать значение целевой функции. Поэтому коэффициенты при дополнительных переменных в целевой функции равны нулю. Развернутая форма записи целевой функции представляется так: Zmax = 4x1+10x2+ 0х3+ 0x4.
5, допускались следующие два случая: а) вся пашня будет использована, тогда х1+х2=5 (и х3 =0); б) если при сложившихся условиях хозяйству невыгодно использовать всю пашню, т.е. х1+х2<5 (и х3>0), то в этом случае х3 показывает неиспользуемую часть пашни. Переменная х4 отражает неиспользованную часть ресурсов труда. Неиспользуемые ресурсы не могут увеличивать значение целевой функции. Поэтому коэффициенты при дополнительных переменных в целевой функции равны нулю. Развернутая форма записи целевой функции представляется так: Zmax = 4x1+10x2+ 0х3+ 0x4.
Поскольку полученный опорный план не является оптимальным (в дальнейшем будет введен формальный признак оптимальности), его нужно улучшить.
Улучшение первого опорного плана. Чтобы произвести продукцию (и соответственно увеличить Z), очевидно, необходимо ввести в число базисных переменных ту, которая обеспечивает наибольший прирост целевой функции Z.
Поскольку наибольший коэффициент в целевой функции при х2, введем ее в базис. Соответственно, одну из переменных нужно вывести из базиса.
Чтобы возрастала целевая функция Z, нужно увеличить х2. Но нельзя увеличивать эту переменную безгранично, так как она связана с другими переменными. Если х2 придать очень большое значение, то другие переменные могут стать отрицательными, что недопустимо по условиям задачи. Предельно допустимое значение х2 можно определить, вычислив так называемые симплексные отношения. Они получаются делением свободного члена каждого уравнения (в канонической записи) на положительный коэффициент при вводимой в базис переменной (т.е. при х2):

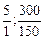 или (5; 2).
или (5; 2).
Минимальное симплексное отношение (2) показывает, что необходимо выводить из базиса в число свободных переменных х4 из второго уравнения. На втором этапе расчетов базисными переменными будут х2, х3, а свободными - переменные х1и х4.
Далее снова базисные переменные выражают через свободные, и расчеты, аналогично изложенным выше, повторяют до тех пор, пока возможно увеличение значения целевой функции. Однако поиск оптимального плана методом логических рассуждений и путем преобразований системы исходных уравнений громоздок и неудобен, хотя и важен для понимания существа метода. Схема расчетов может быть формализована в виде строгого и более простого алгоритма. Наиболее удобно вести решение задачи с использованием специальных так называемых симплексных таблиц.
Построение макета и заполнение первой симплексной таблицы. Первая симплексная таблица представляет форму выражения опорного плана, когда свободные переменные равны нулю, ресурсы не используются и Z=0. Поэтому при заполнении первой таблицы дополнительные переменные считаются базисными (x3, х4), аосновные переменные (х1, х2)– свободными. Каждая строка таблицы отражает соответствующее уравнение системы в канонической форме, хотя столбцы располагаются в иной последовательности, чем достигаются определенные технические удобства в расчетах. Расположение переменных показано в таблице 4.
Таблица 4 – Первая симплексная таблица
| cj | |||||||
| сi | П Б | b0 | x1 | x2 | x3 | x4 | co |
| x3 | |||||||
| x4 |  2 2
| ||||||
 j j
| -4 |
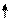 -10 -10
|
В первом столбце записываются коэффициенты целевой функции сj для базисных переменных х3, х4.В первом опорном решении все они равны нулю. Во втором столбце перечислены буквенные символы базисных переменных (х3, х4) и Z. В первой верхней строке таблицы приводятся коэффициенты целевой функции сj при всех переменных.
Во вторую строку записываются буквенные символы всех переменных, причем свободные члены указываются в начале ряда и обозначаются bio. Третья и четвертая строки таблицы заполнены коэффициентами соответствующих уравнений системы, то есть представляют собой ее матрицу, включая единичную подматрицу.
Расположение базисных переменных и свободных членов в рядом стоящих столбцах таблицы позволяет легко читать результат опорного решения при равенстве свободных переменных нулю.
Последняя строка таблицы называется оценочной (или индексной) и содержит оценочные коэффициенты переменных ( 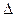 j).
j).
Для х1 оценка равна:
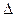 1=(0
1=(0  1+0
1+0  30) – 4 = -4;
30) – 4 = -4;
для х2: 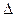 2= (0
2= (0  1 +0
1 +0  150) – 10 = - 10;
150) – 10 = - 10;
для х3 и х4: 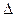 3 = 0;
3 = 0; 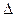 4 = 0.
4 = 0.
Полученные величины занесем в последнюю строку симплексной таблицы.
Последняя строка таблицы соответствует записи приведенной формулы целевой функции, когда все члены с неизвестными перенесены в левую часть уравнения:
Z – 4х1 – 10х2 – 0х3 – 0х4 = 0.
Таким образом, первая симплексная таблица (соответственно и полученное опорное решение) получается непосредственно из канонической формы записи системы.
Определение оптимальности плана. Признак оптимальности.В симплексных таблицах формальным признаком оптимальности является содержание оценочной (индексной) строки. Если задача решается на максимум целевой функции, то план оптимален тогда, когда среди коэффициентов оценочной строки нет отрицательных величин. При решении задачи на минимум признаком оптимальности плана является отсутствие положительных величин среди коэффициентов оценочной строки (при этом коэффициенты в столбце свободных членов не принимаются во внимание).
В первой симплексной таблице все коэффициенты оценочной строки отрицательны или равны нулю. Следовательно, согласно формальному признаку, план (на максимум целевой функции) не является оптимальным и требует улучшения.
Построение новой симплексной таблицы на основе имеющегося опорного решения. При решении задачи на максимум для улучшения опорного плана необходимо ввести в базис ту из свободных переменных, которая в оценочной строке имеет минимальный по величине отрицательный коэффициент (если задача решается на минимум, то в базис вводится переменная с наибольшим положительным коэффициентом). В оценочной строке составленной нами первой симплексной таблицы минимальную оценку (-10) имеет переменная х2.
Столбец, содержащий переменную, которую нужно ввести в базис, называют разрешающим столбцом (k-столбец). В первой симплексной таблице разрешающим является столбец х2 (k=2) .
Если в оценочной строке окажется несколько одинаковых минимальных значений, то в качестве разрешающего выбирается столбец с наименьшим номером.
Чтобы определить, какую из базисных переменных перевести в число свободных, необходимо найти минимальное симплексное отношение путем деления элементов столбца свободных членов (bio) на соответствующие коэффициенты разрешающего столбца (аik). При этом учитывают только неотрицательные отношения. Строка с наименьшим симплексным отношением (разрешающая строка) указывает на переменную, которую следует вывести из базиса и ввести в число свободных.
Рассчитаем по симплексной таблице отношения bio:aik и найдем из них минимальное. По строке х3 находим: 5/1=5; по строке x4: 300/150 = 2.
Определяем минимальное значение из полученных отношений:

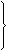 min
min 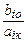 = min {5; 2} = 2.
= min {5; 2} = 2.
Минимальное симплексное отношение находится в строке x4 (r = 4). На пересечении разрешающей строки r и разрешающего столбца k, находится разрешающий элемент (аik) = 150. Разрешающую строку и разрешающий столбец в симплексной таблице выделяют жирными линиями.
Порядок построения второй симплексной таблицы.В заголовке таблицы записывают новые свободные и базисные переменные, по столбцу сi и строке сj указывают их коэффициенты в целевой функции. Вместо разрешающего элемента в новую таблицу записывают 1 ( 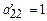 ), а остальные элементы разрешающего столбца, включая и строку оценок, обнуляют (
), а остальные элементы разрешающего столбца, включая и строку оценок, обнуляют ( 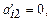 i
i 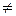 2,
2, 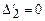 ).
).
Элементы разрешающей строки делятся на разрешающий элемент и получают строку для таблицы 5 с новыми значениями элементов.
Таблица 5 – Вторая симплексная таблица
| cj | |||||||
| сi | П Б | b0 | x1 | x2 | x3 | x4 | co |
| x3 | 4/5 | -1/150 | 3 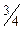
| ||||
| x2 | 1/5 | 1/150 | |||||
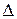 j j
| -2 | 1/15 |
Длястолбца bio имеем 300:150=2,0; для столбца х1 ответственно 30: 150=0,2. По разрешающему столбцу получим аrk =1 и т. д.
Все остальные элементы таблицы (включая и оценки) пересчитывают по правилу «прямоугольника»:
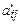 =
= 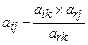 .
.
Для столбца bio по строке х3 получим:
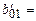 5 -
5 - 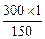 = 3;
= 3;
для оценочной строки:
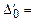 0 -
0 -  = 20.
= 20.
Новые элементы столбца х1 по строке х3:
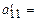 1 -
1 - 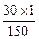 = 0,8;
= 0,8;
для индексной строки:
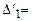 - 4 -
- 4 - 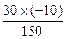 = -2.
= -2.
Поскольку в разрешающей строке элемент равен 0 (а23 = 0), то числитель дроби и вся дробь равна 0, а элементы столбца х3 можно переписать в новую таблицу без изменений.
Столбец х4:
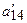 =0 -
=0 - 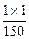 =-1/150;
=-1/150;
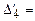 0 -
0 - 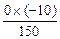 =1/15.
=1/15.
Элементы оценочной (индексной) строки можно вычислить и по формуле, используемой для расчетов в таблице 4.
В оценочной (индексной) строке имеется отрицательный элемент (-2 по столбцу х1).Следовательно, план не является оптимальным. Поэтому столбец х1 в следующей таблице рассматривается как разрешающий, апеременную х1 вводят в базис.
Рассчитаем ивпишем в таблицу 5 значения симплексных отношений (столбец СО). По строке х3:
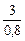 =3,75;
=3,75;
по строке х2:
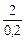 =10.
=10.
 Разрешающей является строка х3,так как минимальное значение СО наблюдается по этой строке:
Разрешающей является строка х3,так как минимальное значение СО наблюдается по этой строке:
min 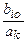 = min {3,75; 10} =3,75.
= min {3,75; 10} =3,75.
Таблица 6 – Третья симплексная таблица (с оптимальным планом)
| cj | ||||||
| сi | П Б | b0 | x1 | x2 | x3 | x4 |
| х1 | 3 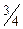
| 1 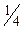
| -1/120 | |||
| х2 | 1 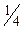
| -1/4 | 1/120 | |||
 j j
| 27,5 | 2,5 | 1/20 |
Результаты расчетов приведены в таблице 6.
В третьей (последней) симплексной таблице нет ни одного отрицательного коэффициента индексной строки. Следовательно, получен оптимальный план. В соответствии с данными таблицы 6, значения базисных переменных, выписанные из столбца bio, равны:
х1= 3,75; х2=1,25.
Согласно оптимальному плану, 3,75 га пашни следует занять зерновыми культурами и 1,25 га – сахарной свеклой. Следовательно, вся пашня и трудовые ресурсы будут использованы полностью. Максимальная стоимость товарной продукции равна 27500 руб.
Дата добавления: 2015-08-14; просмотров: 1470;
