Графический способ решения задачи
Задача линейного программирования в простейшем случае может быть решена графическим способом. Он применим при решении задач небольшой размерности, когда число переменных не превышает трех.
Рассмотрим сельскохозяйственную задачу из темы 2:
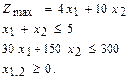
Для решения рассматриваемой задачи построим прямоугольную систему координат. По оси абсцисс (горизонтальная ось) отложим возможные значения переменной х1, а по оси ординат (вертикальная ось) – возможные значения переменной x2. Эти оси разбивают плоскость на четыре квадранта (рис. 2). Определим на графике область допустимых решений задачи, т.е. множество допустимых вариантов плана.

|


| |
 2
2
 |  |

2 4 6 х1
Рис. 2 - Построение граничной прямой
1. Искомые площади под сахарной свеклой и зерновыми культурами не могут быть отрицательными. Следовательно, допустимыми являются только варианты, находящиеся в I квадранте. По условиям задачи пашня составляет 5 га; это ограничение было записано как неравенства х1+х2  5. Такое неравенство делит I квадрант на две полуплоскости, на одной из которых все точки ему удовлетворяют, на другой – не удовлетворяют. Разделительная прямая между полуплоскостями называется граничной прямой. Все точки этой прямой удовлетворяют равенству х1+х2=5. Следовательно, достаточно построить прямую, соответствующую данному уравнению, как полуплоскости будут определены.
5. Такое неравенство делит I квадрант на две полуплоскости, на одной из которых все точки ему удовлетворяют, на другой – не удовлетворяют. Разделительная прямая между полуплоскостями называется граничной прямой. Все точки этой прямой удовлетворяют равенству х1+х2=5. Следовательно, достаточно построить прямую, соответствующую данному уравнению, как полуплоскости будут определены.
Для построения прямой необходимо найти любые две ее точки. Приравняв одну из переменных нулю, определим значение другой: при х1=0, х2=5; при х2=0, х1=5.
Итак, граничная прямая, соответствующая неравенству х1+х2  5, проходит через точки с координатами (0; 5) и (5; 0). Нанесем граничную прямую на график (рис. 2).
5, проходит через точки с координатами (0; 5) и (5; 0). Нанесем граничную прямую на график (рис. 2).
Определим, какая из полуплоскостей включает начало координат (х1=0, х2=0). Подставив в неравенство х1+х2 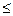 5 значения х1=0 и х2=0, получим 0<5, т.е. начало координат удовлетворяет неравенству. Это значит, что и все точки полуплоскости, включающей начало координат, удовлетворяют неравенству. На рисунке 2 эта полуплоскость показана стрелками от граничной прямой.
5 значения х1=0 и х2=0, получим 0<5, т.е. начало координат удовлетворяет неравенству. Это значит, что и все точки полуплоскости, включающей начало координат, удовлетворяют неравенству. На рисунке 2 эта полуплоскость показана стрелками от граничной прямой.
2. Рассмотрим на графике второе неравенство, отражающее ограничение по трудовым ресурсам: 30x1+150x2 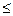 300. Чтобы найти граничную прямую, заменим неравенство на уравнение: 30x1+150x2=300. Приняв x1=0, получим: 150x2=300, откуда x2=2. Следовательно, граничная прямая второго неравенства проходит через точку (0; 2). Находим вторую точку этой граничной прямой, приравняв x2 нулю: 30x2=300, откуда x1=10. Следовательно, вторая точка, через которую проходит граничная прямая, имеет координаты (10; 0).
300. Чтобы найти граничную прямую, заменим неравенство на уравнение: 30x1+150x2=300. Приняв x1=0, получим: 150x2=300, откуда x2=2. Следовательно, граничная прямая второго неравенства проходит через точку (0; 2). Находим вторую точку этой граничной прямой, приравняв x2 нулю: 30x2=300, откуда x1=10. Следовательно, вторая точка, через которую проходит граничная прямая, имеет координаты (10; 0).
Экономический смысл рассматриваемых величин состоит в следующем: имеющиеся трудовые ресурсы (300 чел.–дн.) позволяют возделывать либо 2 га сахарной свеклы (при этом 3 га пашни остались бы неиспользованными), либо 10 га зерновых культур (но в хозяйстве имеется всего 5 га пашни).
х2 

 6
6

 4 (1)
4 (1)
|
|


|
|
 2
2
|












0 2 4 6 8 10 х1
Рис. 3 - Определение области допустимых решений задач
Нанесем на график (рис. 3) найденные точки с координатами (0; 2) и (10; 0), соединим их прямой (2), являющейся граничной для неравенства, выражающего ограничение по трудовым ресурсам.
Определим, какая полуплоскость удовлетворяет этому неравенству. Приняв х1=0 и х2=0, убедимся в том, что неравенству удовлетворяет полуплоскость, расположенная ниже граничной прямой (эта полуплоскость включает начало координат, так как при х1=0 и х2=0 имеем 0<300).
Граничные прямые системы неравенств (1,2), нанесенные на график, отсекают на плоскости I квадранта выпуклый многоугольник OABC (рис.3). Любая точка данного многоугольника (включая и точки, лежащие на его граничной прямой) удовлетворяет одновременно всем ограничениям задачи. Поэтому множество точек этого многоугольника представляет собой область допустимых решений (ОДР) задачи (допустимых вариантов плана).
В теории линейного программирования доказывается, что экстремальное значение целевой функции обязательно достигается на границе выпуклого многогранника с конечным числом угловых точек. Такой многогранник называется симплексом. Отсюда произошло название симплексного метода решения задач линейного программирования путем направленного перебора вершин симплекса до получения оптимального плана. Следовательно, оптимальный вариант плана можно отыскать, последовательно перебирая варианты сочетания х1 и х2 на вершинах многоугольника. Определим по графику (рис. 3) координаты вершин многоугольника и найдем соответствующие значения целевой функции (табл. 3).
Таблица 3 – Значение переменных и условий функции
в задаче линейного программирования
| Вершина ДОР | Координаты | Значение целевой функции, тыс. руб. |
| O | 0; 0 | |
| А | 0; 2 | |
| В | 3 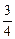 , 1 , 1 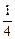
| 27,5 |
| С | 5; 0 |
Таким образом, максимальное значение целевой функции достигается в вершине В, что соответствует варианту плана, когда площадь зерновых (х1) составляет 3,75 га и площадь сахарной свеклы (х2) – 1,25 га.
Однако решение задачи путем последовательного рассмотрения всех вершин многоугольника трудоемко. Более эффективен следующий способ. Возьмем целевую функцию задачи Zmax=4x1+10x2. Ей можно придать любое произвольное значение (например, вычислив или приблизительно определив значение Z для любой точки многоугольника допустимых решений задачи). Допустим, Z=20 тыс. руб., т.е. Z=4х1+10х2=20. Построим на графике прямую, соответствующую этому уравнению. При х1=0 имеем 10х2=20, откуда х2=2; при х2=0 имеем 4х=20, откуда х1=5. Следовательно, прямая, соответствующая уравнению 4х1+10х2=20 проходит через точки с координатами (0; 2) и (5; 0) (рис. 4). Прямую, соответствующую целевой функции, называют линией уровня (разрешающей линией).
 х2
х2
|
|
|



 |









0 2 4 С 6 х1
Рис. 4 - Графический метод решения задачи линейного программирования
Поскольку экстремальное значение целевой функции обязательно достигается на поверхности выпуклого многогранника, то следует передвигать разрешающую линию параллельно самой себе до тех пор, пока она не коснется крайней точки выпуклого многогранника. В рассматриваемом примере такой точкой является вершина В (рис. 4). Координаты найденной вершины и соответствуют оптимальному варианту плана.
Иногда разрешающая линия может совпадать с одной из сторон многоугольника. Это означает, что данная задача имеет не одно, а множество оптимальных решений, так как координаты любой точки данной стороны многоугольника будут приводить к одному и тому же значению целевой функции.
Удобным и простым способом нахождения точки экстремума целевой функции является определение вектора-градиента, который показывает направление максимизации целевой функции. Чтобы построить вектор-градиент на графике, достаточно определить две точки. Начальная точка вектора-градиента совпадает с началом координат. В качестве координат конечной точки вектора-градиента принимаются коэффициенты целевой функции (4; 10)1.
Из теории линейного программирования известно, что вектор-градиент и разрешающая линия взаимно перпендикулярны. Передвигая разрешающую линию параллельно самой себе по направлению вектора-градиента, можно найти крайнюю точку В выпуклого многогранника, соответствующую оптимальному плану.
Дата добавления: 2015-08-14; просмотров: 1023;
