Задача линейного программирования

Линейное программирование является частным разделом математического программирования. Математическое программирование – направление прикладной математики, в котором изучаются задачи условной оптимизации. В экономике такие задачи возникают при практической реализации принципа оптимальности в планировании и управлении.

Необходимым условием оптимального подхода к планированию и управлению (принципа оптимальности) является гибкость, альтернативность производственно-хозяйственных ситуаций, в условиях которых приходится принимать планово-управленческие решения.

Суть принципа оптимальности состоит в стремлении выбрать планово-управленческое решение, заданное вектором 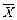= (х₁, х₂,…х_n), где х_j (j = 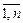) – его компоненты, которое наиболее адекватно отражает внутренние возможности и внешние условия производственной деятельности хозяйствующего субъекта.

Понятие «наиболее адекватно» здесь означает применение некоторого критерия оптимальности, соответствующего экономическому показателю сравнения эффективности вариантов планово-управленческих решений. Традиционные критерии оптимальности: «максимум прибыли» и «минимум затрат».

Оценка внутренних возможностей и внешних условий производственной деятельности заключается в выполнении экономических условий, т.е. выбор X осуществляется из некоторой области возможных (допустимых) решений D; которую называют областью определения задачи.

Принципу оптимальности в планировании и управлении отвечает решение экстремальной задачи вида:

max (min) f ( 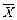), (1)

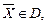(2)

где f ( 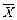) – математическая запись критерия оптимальности – целевая функция.

Задачу условной оптимизации (1) - (2) обычно записывают в виде:

Найти максимум или минимум функции

f ( 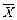) = f (х₁, х₂,…х_n) (3)

при ограничениях

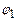( х₁, х₂,…х_n) {<,=,>}b₁ (4)

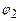( х₁, х₂,…х_n) {<,=,>}b₂

............................................

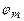( х₁, х₂,…х_n) {<,=,>}b_m

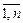x_j 0, j= . (5)

Обозначение {<,=,>} говорит о том, что в конкретном ограничении возможен один из знаков: <,= или >. Более компактная запись:

max (min) f (х₁, х₂,…х_n), (6)

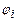( х₁, х₂,…х_n) {<,=,>} b_i , i= 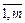, (7)

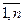x_j 0, j= . (8)

Задача (6) - (8) называется общей задачей математического программирования, другими словами, математической моделью задачи оптимального планирования, в основе построения которой лежат принципы оптимальности и системности.

Вектор 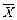(набор управляющих переменных x_j, (j = 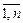) называется допустимым решением, или планом задачи математического программирования, если он удовлетворяет системе ограничений. Допустимый план Х, который позволяет достичь максимум или минимум целевой функции f(x₁, х₂, ..., х_n), называется оптимальным планом (оптимальным вариантом, или просто решением) задачи оптимального программирования.

Выбор оптимального управленческого решения в конкретной производственной ситуации связан с прове дением с позиций системности и оптимальности экономико-математического моделирования и решением задачи оптимального программирования.

Задачи математического программирования классифицируют по следующим признакам.

1. По характеру взаимосвязи между переменными:

а) линейные – все соотношения заданы линейными функциями;

б) нелинейные – наличие нелинейных функций.

2. По характеру изменения переменных:

а) непрерывные, область допустимых значений образуют действительные числа;

б) дискретные – требование целочисленности некоторых переменных.

3. По учету фактора времени:

а) статические,

б) динамические.

4. По наличию информации о переменных:

а) задачи в условиях полной определенности (детерминированные),

б) задачи в условиях неполной информации,

в) задачи в условиях неопределенности.

5. По числу критериев оценки альтернатив:

а) однокритериальные задачи,

б) задачи с использованием многокритериального комплекса.

Наиболее изучены задачи линейного программирования, для которых разработан универсальный метод решения, реализуемый способом последовательного улучшения плана (симплекс-метод), с помощью которого может быть решена любая задача линейного программирования.