Классификация экономико-математических методов

Особенностью решения задач управления экономикой является необходимость учета при их решении множества переменных величин, характеризующих постоянно изменяющиеся производственные условия.

Так как число сочетаний этих величин в течение определенного времени могло быть достаточно большим, то возможно существование значительного числа вариантов решений. Отсюда большая размерность решаемых задач. В этих условиях простой перебор и сравнение всех возможных вариантов решения конкретной задачи нереально из-за большой трудоемкости вычислений. Поэтому требуются специальные методы, позволяющие достаточно быстро и с достаточной степенью обоснованности найти искомое решение. Эти методы получили название экономико-математических методов.

Поскольку целью изучения экономико-математических методов является раскрытие механизма их реализации, определение области наиболее эффективного использования, то в качестве классификационного признака можно принять, например, характер используемого математического аппарата. По этому признаку можно выделить методы классической и прикладной математики (рис.1).

Методы классической математики включают математический анализ и теорию вероятностей. Методы математического анализа в свою очередь могут быть классифицированы на дифференциальное и вариационное исчисления. Эти методы целесообразно использовать при расчете параметров календарно-плановых нормативов: определение размеров партии деталей, длительности производственного цикла, для оперативного регулирования производства и др.

Группа методов прикладной математики обширна по номенклатуре, неоднородна по составу элементарных расчетов, способам их реализации, применяемым приемам и т.д. По общности указанных признаков методы рассматриваемой группы можно классифицировать следующим образом: методы оптимального программирования, математической статистики, комбинаторные методы, теории расписаний, игр, массового обслуживания, управление запасами, метод экспертных оценок.

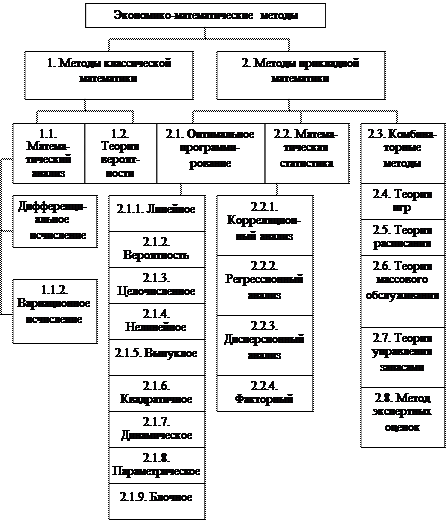
Рис. 1 – Классификация экономико-математических методов

Методы математической статистики используются для нахождения и раскрытия закономерностей, свойственных большим совокупностям однородных объектов. При этом изучается не каждый элемент совокупности, а определенная выборка. Полученные характеристики такой выборки могут использоваться: 1) для сравнительной оценки элементов различных совокупностей или их характеристик, 2) для установления связей между отдельными величинами, 3) для прогнозирования на этой основе развития системы в будущем. Математическая статистика включает: корреляционный, регрессионный, дисперсионный, факторный анализы и др.

Оптимальное программирование – это комплекс специальных методов, обеспечивающих в условиях множества возможных решений выбор такого, которое является наилучшим (оптимальным) по заданному критерию при определенных ограничивающих условиях. Оптимальное программирование – эффективный инструмент решения задач управления. В их числе: линейное, вероятностное, целочисленное (дискретное) программирование, нелинейное, выпуклое, квадратичное, динамическое, параметрическое, блочное и др.

В математике решаемые на оптимум задачи называются экстремальными. В них требуется отыскать максимум или минимум некоторой целевой функции.

Линейное программирование используется при решении задач в том случае, когда целевая функция и ограничения выражены линейными зависимостями. Эти методы в настоящее время являются наиболее разработанными, относительно простыми и понятными для широкого использования. Существуют эффективные алгоритмы для использования вычислительной техники при их реализации. Многие процессы допускают линейную интерпретацию, а некоторые нелинейные зависимости могут быть сведены к линейным для ограниченного числа ситуаций.

Однако в некоторых случаях применение линейных методов искажает получаемые результаты, что приводит к необходимости использования и других методов.

Если в системе равенств или неравенств содержатся случайные элементы, но зависимости между переменными линейные, то такая задача решается методами вероятностного программирования. Если при нахождении неизвестных переменных необходимо, чтобы одна из них или несколько принимали только целочисленные значения, то в этом случае при решении такой задачи необходимо использовать методы целочисленного программирования.

Методы нелинейного программирования используются тогда, когда целевая функция, или хотя бы одно ограничение, выражены нелинейной зависимостью. В числе методов нелинейного программирования можно выделить квадратичное и выпуклое программирование.

Выпуклое программирование представляет собой совокупность специальных методов решения нелинейных экстремальных задач, у которых выпуклы либо целевая функция, либо ограничительные условия.

Квадратичное программирование – это совокупность методов решения особого класса экстремальных задач, в которых ограничения линейны, а целевая функция является многочленом второй степени.

Методы динамического программирования могут применяться для решения оптимизационных задач, в которых необходимо рассматривать процесс управления или производства в пространстве или во времени, т.е. в развитии. Весь процесс поиска оптимального решения представляется в виде определенной последовательности шагов, для каждого из которых находится оптимальное решение, влияющее на последующие шаги (принцип многошаговости Р.Беллмана).

В моделях реальных экономических систем коэффициенты целевой функции или ограничения могут являться не постоянными величинами, а изменяться в течение определенного периода времени под воздействием различных факторов. В этом случае эффективными будут методы параметрического программирования.

Модели, содержащие большое число показателей, очень сложны в реализации. Поэтому в тех случаях, когда это возможно, их преобразуют в несколько моделей меньшей размерности. Полученные локальные задачи решаются совместно с использованием специальных методов, наиболее известным из которых является метод разложения Данцига-Вульфа. Это методы блочного программирования.

Для решения задач методами математического программирования используются комбинаторные методы, например, ветвей и границ. В случае «трудной» задачи она заменяется на набор задач, представляющих ветвь. Чем больше ветвей, тем большее значение получает целевая функция. Граница предельной ветви достигается в том случае, если значение критерия не улучшается. К этим методам близко подходят эвристические, основные на опыте, интуиции исполнителя.

Когда приходится принимать решения в условиях неопределенноcти, причем такое решение должно обеспечивать наибольший эффект или наименьшие потери, целесообразно пользоваться методами теории игр.

Предметом исследования теории массового обслуживания являются вероятностные модели реальных систем обслуживания, в которых в случайные моменты времени возникают заявки на обслуживание и имеются устройства для обслуживания этих заявок. В экономике: заявка – спрос на продукцию определенного вида, обслуживающее устройство – предприятия.

Теория расписаний представляет собой систему методов, позволяющих упорядочить во времени использование системы машин для обработки некоторого множества изделий. При этом должны быть выполнены определенные технологические условия и обеспечено достижение оптимального значения заранее заданного критерия качества расписания.