Симплексный метод и его алгоритм

Универсальным аналитическим алгоритмом решения задач линейного программирования является симплексный метод (или симплекс-метод). Идея этого метода основывается на том, что вначале получают допустимый вариант, удовлетворяющий всем ограничениям, а оптимальное решение - достигается последовательным улучшением первого опорного плана за конечное число этапов-итераций. Нахождение первоначального решения и переход к следующему опорному плану проводятся методом
Жордана-Гаусса для системы линейных уравнений в канонической форме

¹Это справедливо только в случае, когда целевая функция линейна. Координаты конечной точки вектора-гра­диента определяются как частные производные целевой функции по координатам: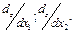

записи исходной ЗЛП, а направление перехода от одного опорного решения к другому выбирается на основе некоторого математического критерия оптимальности. Симплекс-метод базируется на следующих свойствах ЗЛП:

1) Не существует локального экстремума, отличного от глобального.

2) Множество всех планов задачи линейного программирования являются выпуклыми.

3) Целевая функция ЗЛП достигает своего максимального (минимального) значения в угловой точке многогранника решений.

4) Опорные планы ЗЛП размещаются в угловых точках симплекса.

Наиболее проста вычислительная схема симплекс-метода с естественным базисом. Для применения этого метода ЗЛП должна быть сформулирована в канонической форме (12) - (14), причем матрица системы уравнений должна содержать единичную подматрицу размерностью m х m.

Предположим, что первые m векторов системы составляют единичную матрицу. Тогда первоначальный опорный план очевиден (b₁, b₂,…,b_m, 0,…,0).

Далее используется математический критерий для проверки на оптимальность первого опорного плана. Переход к последующему опорному плану выполняется с помощью преобразований Жордана-Гаусса и с использованием критерия оптимальности.

Далее полученный опорный план вновь проверяется на оптимальность. Вычислительный процесс заканчивается за конечное число шагов, причем на последнем шаге выявляется неразрешимость задачи либо достигается оптимальное решение и соответствующее ему экстремальное значение целевой функции.

Признаками оптимальности являются следующие утверждения:

1) Если для некоторого вектора, не входящего в базис, выполняется условие:

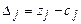<0, где 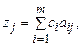j= ,

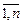то можно получить новый опорный план, для которого значение целевой функции будет больше исходного; при этом могут быть два случая:

а) если все координаты вектора, подлежащего вводу в базис, неположительные, то ЗЛП не имеет решения;

б) если имеется хотя бы одна положительная координата у вектора, подлежащего вводу в базис, то можно получить новый опорный план.

2) Если для всех векторов выполняется условие 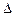_j = Zj - Cj 0, то полученный план является оптимальным.

На основании признака оптимальности в базис вводится вектор A_k, давший минимальную отрицательную величину симплекс-разности:

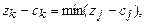
Чтобы выполнялось условие неотрицательности значений опорного плана, из базиса выводится вектор А_r, который дает минимальное положительное симплексное отношение

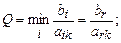
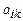>0, i= .

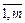Строка А_r и столбец А_к называются направляющими (разрешающими), а элемент а_rk – ключевым (разрешающим).

Элементы вводимой строки, соответствующей направляющей строке, в новой симплекс-таблице вычисляются по формулам:

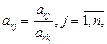
а элементы любой другой i-й строки пересчитываются по формулам:

Значения базисных переменных нового опорного плана рассчитываются по формулам:

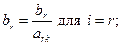
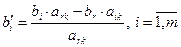для .