Явления переноса

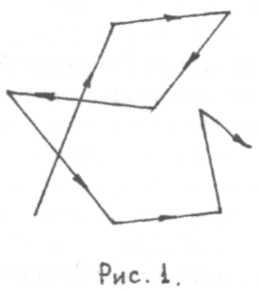
1. Средняя длина свободного пробега молекул. В связи с тем, что молекулы газа движутся хаотически и испытывают со­ударения между собой, траектория их движения может быть представлена ломаной линией (рис. 1).

Расстояния, проходимые молекулами от одного соударения до другого, различны, однако, можно ввести понятие средней длины свободного пробега λ. Средней длиной свободного про­бега молекулы называют среднее расстояние, проходимое моле­кулой между двумя последовательными столкновениями.

Имея среднюю скорость движения v, молекула за 1 секунду

проходит путь

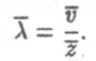и за это время она испытывает z столкновений. Тогда

Расчеты показывают, что

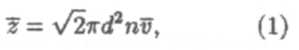
где n — концентрация молекул, a d — диаметр молекулы. Если учесть, что d = 2R, то z = 4 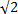πr²nv.Тогда мы получаем формулу для средней длины свободного пробега

Оценим значения г и А при нормальных условиях.

Полагая r = 2*10^-10м, п = 2,7• 10²⁵ м^-3, Т = 273 К, р = 10⁵Па и v = 5 * 10² м/с, получим, что

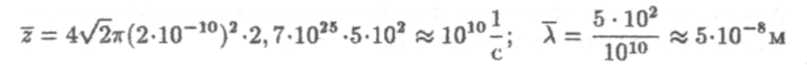
Как было показано в молекулярно-кинетической теории, кон­центрация молекул

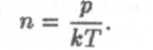
Подставляя в формулу (2), получим

Следовательно, при постоянной температуре (T = const) по ме­ре разрежения газа, т.е. уменьшения его давления, средняя дли­на свободного пробега возрастает, так что

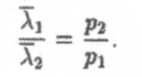
Уменьшая давление газа, можно достичь такого состояния, что средняя длина свободного пробега станет равной размерам со­суда, в котором находится газ. Это означает, что молекулы будут пролетать от одной стенки до другой практически без столкновений с другими молекулами.

Такая область давлений называется вакуумом. Например, в лабораторной колбе размером 10 см (λ= 0,1 м) при Т = 273 К вакуум наступает при давлении около 5 • Ю^-2 Па.

2. Понятие градиента Физической величины Физические ве­личины могут изменяться не только с течением времени, но и быть различными в различных точках пространства. Пред­ставим себе, что некоторая физическая величина φ возрастает вдоль направления оси х (рис. 2).

Тогда градиентом физической величины называется вектор­ная величина, равная отношению изменения величины к рассто­янию, на котором она изменяется.

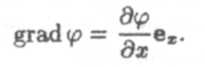
Градиент всегда направлен в сторону наибольшего возрастания функции. Очевидно, что, если функция возрастает, то grad ip > 0; если функция убывает, то grad</> < 0.

3. Явления переноса. Равновесныл< называется такое состо­яние системы, при котором ее термодинамические параметры (p,V,T) остаются неизменными сколь угодно долго. При этом наблюдается полная хаотичность движения молекул, распреде­ление которых по скоростям подчиняется распределению Макс­велла. Если равновесие системы нарушено, то она стремится самопроизвольно вернуться к состоянию равновесия. Поэтому появляются направленные потоки частиц, с которыми перено­сятся из одной части газа в другую масса, энергия и импульс. Эти процессы в газе называются явлениями переноса. К ним от­носятся диффузия, теплопроводность и внутреннее трение (вяз­кость). Первоначально они были исследованы опытным путем, и были получены эмпирические формулы (т.е. формулы, полу­ченные на основании наблюдений и измерений, а не теоретиче­ских выкладок). Впоследствии эти формулы получили теоре­тическое обоснование. Рассмотрим подробнее каждое из этих явлений.

а) Диффузия — это самопроизвольное выравнивание концен­траций (плотностей) в смеси нескольких веществ.

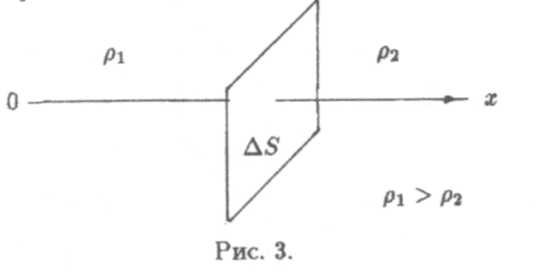
Пусть в некотором объеме газа его плотность р уменьшается в направлении оси х (рис. 3). Через площадку ∆S, перпендикулярную

оси х, будет идти поток частиц, вместе с которым будет переноситься масса газа ∆М. Установлено, что

масса газа, перекосимая при диффузии через площадку, перпен­дикулярную направлению ОХ, в котором убывает плотность, пропорциональна площади этой площадки, промежутку времени переноса и градиенту плотности

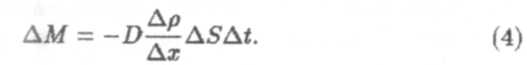
Это уравнение диффузии или закон Фика,где D — коэффициент диффузии газа. Если положить ∆р/∆х = -1 кг/м⁴, ∆S = 1 м² и ∆t = 1 с, то ∆М = D и можно сказать, что коэффициент диффузии численно равен массе газа, переносимой через площадку 1 м² за 1 с при градиенте плотности -1 кг/м⁴. [D] = м²/с.

Знак "минус" в законе показывает, что перенос массы идет в направлении уменьшения плотности.

Диффузия очень широко распространена в природе. Процес­сы дыхания растений через листья, мелких организмов через покров, животных через легкие, всасывание при пищеварении идут с помощью диффузии. Диффузия является основным ме­ханизмом, обеспечивающим газообмен между почвенным и ат­мосферным воздухом. Кроме того, в отсутствии диффузии про­изошло бы расслоение атмосферы на составляющие фракции.

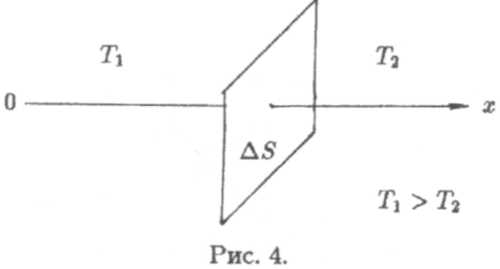
б) Теплопроводность. Пусть в некотором объеме газа темпе­ратура Т убывает в направлении ОХ (рис. 4). Через площадку ∆S, перпендикулярную ОХ, будет идти поток частиц, которыми будет переноситься энергия в виде количества теплоты ∆Q.

Установлено, что

количество теплоты, переносимое через площадку, перпенди­кулярную направлению ОХ, пропорционально площади этой площадки,

промежутку времени переноса и градиенту температу­ры

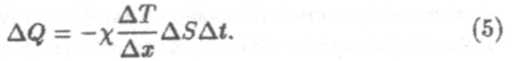
Это уравнение теплопроводности или закон Фурье, где χ— ко­эффициент теплопроводности газа. Если положить ∆Т/∆х = -1 К/и, AS - 1 м² и At - 1 с, то AQ = х,т.е. коэффициент те­плопроводности численно равен количеству теплоты, переноси­мому сквозь площадку 1 м² за 1 с при градиенте температуры -1 К/м. [χ] - Дж/(м • с • К).

У сильно разреженных газов теплопроводность хпропорци­ональна давлению. Это используется в термосе (сосуде Дьюара), в котором жидкость долго сохраняет свою температуру за счет слабой теплопроводности разреженного пространства между его двойными стенками. Закон Фурье необходимо учи­тывать при проектировании оконных и дверных проемов зданий для сохранения тепла в них. Также теплопроводность имеет важное значение в поддержании теплового баланса живых ор­ганизмов.

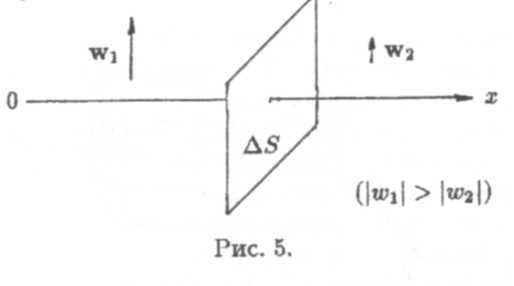
в) Внутреннее трение (вязкость). Пусть в ламинарном пото­ке газа скорость течения w убывает в направлении ОХ. Вообра­зим, что вдоль площадки ∆S (рис. 5) движутся два соприкаса­ющихся слоя газа с различными скоростями (w₁ > w₂). Мо­лекулы левого слоя будут обладать большим импульсом, чем молекулы правого (mw₁ > тw₂), в результате чего через пло­щадку будет переноситься импульс силы F∆t, что приводит к появлению силы трения между двумя слоями. В результате вну­треннего трения более быстрый слой тормозится, а медленный — ускоряется.

- Установлено, что

импульс силы, переносимый через площадку, вдоль которой

скользят друг относительно друга два слоя газа, пропорционален градиенту скорости слоев, площади их соприкосновения и време­ни скольжения

Если сократить это равенство на ∆t, получится уравнение для силы внутреннего трения

Его называют законом Ньютона, где п — коэффициент внутрен­него трения (вязкость). Если положить ∆w/∆x = -1 см^-1, а ∆S = 1 см², то F = 𝛈, т.е.

вязкость численно равна силе внутреннего трения между двумя движущимися слоями при площади их соприкосновения 1 м² и при градиенте скорости -1 с^-1. [𝛈]- кг/(м* с).

Необходимо отметить, что закон Ньютона часто применяет­ся для жидкостей и используется как один из основных в гидро­динамике.

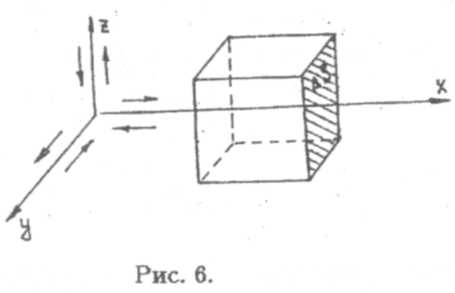
г) Общее уравнение переноса. Рассмотрение законов Фика, Фурье и Ньютона позволяет увидеть много общих черт в явле­ниях переноса; условия возникновения явления, внешний вид за­кона. Это позволяет предположить, что существует общее уни­версальное уравнение переноса. Попробуем вывести его, исхо­дя из представлений молекулярно-кинетической теории. Опре­делим прежде всего количество молекул, проходящих за про­межуток времени ∆t через некоторую воображаемую площадку ∆S, помещенную в газе (рис. 6).

Ориентируем ось ОХ перпендикулярно площадке ∆S. Вви­ду хаотичности движения молекул допустим (как и при выводе уравнения Клаузиуса), что вдоль этой оси пройдет 1/3 всех мо­лекул, из них в положительном направлении оси ОХ — 1/6 от общего числа. При средней скорости v они проходят рассто­яние v * ∆t. Тогда за ∆t через площадку ∆S перейдет слева направо 1/6 всех молекул, находящихся в объеме прямоуголь­ного параллелепипеда с основанием ∆S и высотой, равной v∆t, т.е. N = 1/6 (п * ∆S * v * ∆t), где п —концентрация молекул. Эти молекулы переносят с собой через площадку и значения сво­их физических характеристик (массу, энергию, импульс и т.п.). Пусть эта переносимая характеристика будет φ. Тогда в од­ном направлении через площадку ∆S будет перенесено общее количество этой характеристики

Пусть теперь рассматриваемый газ будет неоднороден по своим свойствам и количество nφ убывает в положительном направле­нии оси ОХ (рис. 7)

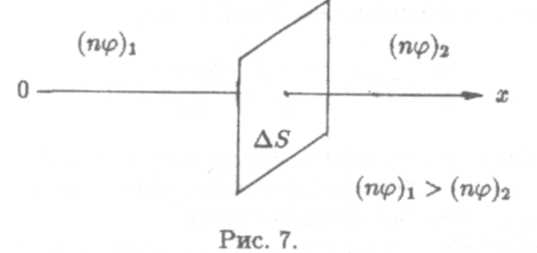
В этом случае будет иметь место преимущественный перенос физической величины Nφ через площадку слева направо.

Он равен

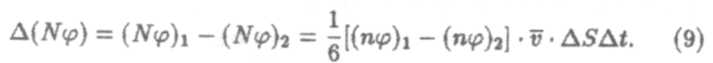
Так как обмен значениями φ и изменение концентрации п происходит только при взаимостолкновениях молекул, т.е. на рассто­янии λ, равном средней длине свободного пробега молекул, то можно положить, что значения (nφ) сохраняются неизменными

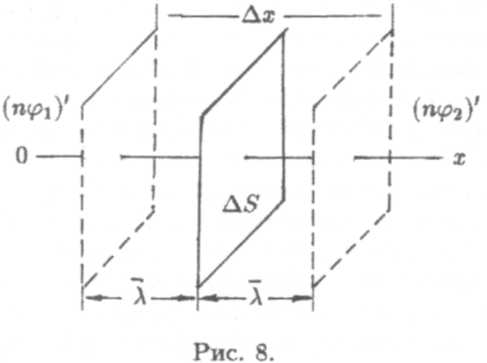
на расстоянии λ влево и вправо от площадки, а изменение ∆(nφ) происходит на расстоянии ∆х = 2λ (рис. 8).

Умножим и разделим правую часть формулы (9) на 2λ, тогда

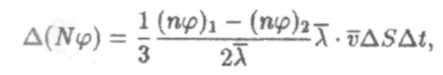
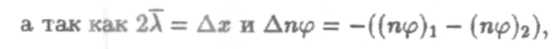
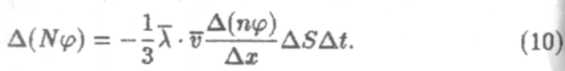
Эта формула и есть общее уравнение переноса.Уравнения диффузии, теплопроводности и внутреннего трения могут быть получены из него как частные случаи.

а) Диффузия, φ=m_o (т_о — масса молекулы). Тогда

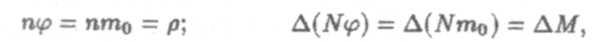
а уравнение (10) принимает вид

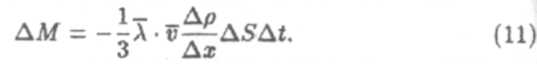
Принимаем

и получаем уравнение Фика, (4).

б) Теплопроводность. φ — (i/2)kT (кинетическая энергия мо­лекулы газа), ∆(N<φ) = ∆(Nw) = ∆Q. Легко показать, что

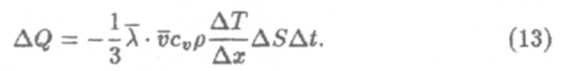
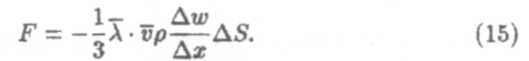
Обозначим

приходим к уравнению Ньютона (7).

Из формул (12),(14) и (16) следуют соотношения коэффициентов переноса

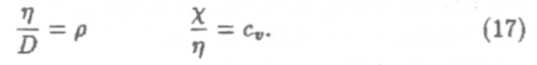
Эти выражения, а также уравнения (11),(13) и (15) находятся в полном соответствии с опытными данными и эмпирическими формулами, что является лучшим подтверждением правильно­сти рассмотренной нами молекулярно-кинетической теории.

Лекция № 15