Эффект Джоуля-Томсона

Рассмотрим экспериментальную установку, изображенную на рис. 5 (Джоуль и Томсон, 1852-1862). Из сосуда 1, где под­держивается давление p₁, газ медленно перетекает через пори­стую пробку П (вата) в сосуд 2 с давлением p₂ (p₂ < p₁). Си­стема теплоизолирована (приток тепла Q = 0). Считаем, что тепловое равновесие между газом и пробкой установилось.

Стационарное течение газа через пористую пробку при указанных условиях называется течением Джоуля-Томсона.

Будем измерять температуры Т₁ и Т₂ по обе стороны от проб­ки. Легко видеть, что некоторая масса газа, занимавшая сле­ва от пробки объем V₁, а после протекания занявшая объем V₂ справа от нее (см. рис. 5), совершила работу А = p₂V₂ — p₁ V₁.

Первое начало термодинамики позволяет нам определить из­менение внутренней энергии этой порции газа:

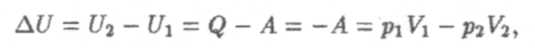
или U₁ + p₁V₁ = U₂ + p₂V₂.Величина I = U + pV носит название энтальпии. To есть, при течении Джоуля-Томсона энтальпия сохраняется.

Для идеального газа p₂V₂= p₁V₁(закон Бойля-Мариотта). Значит, А = 0 и ∆U= 0 — при таких условиях внутренняя энергия идеального газа не меняется. А внутренняя энергия идеального газа совпадает с суммарной кинетической энергией всех его молекул W_k, которая зависит только от температуры: W_k = CvT (здесь Сv — молярная теплоемкость газа при посто­янном объеме). Поэтому при проведении описанного опыта над идеальным газом температура не должна изменяться: Т₁ = Т₂. Однако Джоуль и Томсон обнаружили изменение температуры.

Эффект Джоуля-Томсона состоит в изменении температуры газа при течении Джоуля- Томсона.

Большинство газов охлаждались при таком расшире­нии: Т₂ < T₁ (положительный эффект Джоуля-Томсона). Водо­род же, напротив, нагревался: Т₂ < T₁ (отрицательный эффект Джоуля-Томсона). Модель идеального газа не в силах объяс­нить рассмотренный эффект.

Эффект Джоуля-Томсона применяется, например, в маши­не Линде для получения жидкого воздуха. Воздуху, сжатому первоначально примерно до 100 атм, дают резко расшириться. Так как знак эффекта Джоуля-Томсона в этом случае положи­телен, температура снижается, что позволяет охладить новую порцию сжатого воздуха, которому опять дают расшириться, и так далее. На каком-то этапе температура очередной порции становится столь низкой, что воздух ожижается.

В изложенных ранее главах молекулярно-кинетической тео­рии мы имели дело с моделью идеального газа. Идеальный газ состоит из беспорядочно движущихся молекул, причем предпо­лагается, что:

• Можно пренебречь размерами молекул по сравнению с меж­ молекулярными расстояниями.

• Молекулы не взаимодействуют друг с другом на расстоя­нии. При непосредственном столкновении молекул они взаи­модействуют как абсолютно упругие шары.

Идеальный газ в точности подчиняется экспериментальным законам Бойля-Мариотта, Шарля и Гей-Люссака. Уравнение со­стояния одного моля идеального газа имеет вид:

— уравнение Менделеева-Клапейрона (здесь V_μ - объем одного моля газа). Однако опыт Эндрюса показал, что для реальных газов соотношение (1) выполняется лишь приближенно, да и то если температура превышает критическую. Модель идеального газа даже качественно не описывает переход из газообразного в жидкое состояние. Таким образом, для более точного описа­ния свойств реального газа следует отказаться от упрощающих положений, сформулированных вначале, введя в уравнение (1) следующие поправки:

• Поправка на наличие собственных размеров молекул.

• Поправка на межмолекулярное взаимодействие не только при непосредственном столкновении, но и но расстоянии. Рассмотрим наиболее простой и естественный путь получе­ния уравнения состояния реального газа (Ван-дер-Ваальс, 1873).