Поправка на межмолекулярное взаимодействие
Между молекулами действуют как силы притяжения, так и отталкивания (см. рис. 6). Однако силы отталкивания становятся заметными только при очень малых межмолекулярных расстояниях (фактически, при столкновении), в остальных случаях отталкивание пренебрежимо мало.
Таким образом, можно утверждать, что молекулы притягиваются. Заметим, что молекула, находящаяся вдали от стенки сосуда, в который помещен газ, окружена другими молекулами со всех сторон (молекула I на рис. 6) и сумма всех действующих на нее сил притяжения FI равна нулю. Молекулы же тонкого пристеночного слоя (II на рис. 6) имеют соседей лишь с внутренней стороны. Поэтому на них действует некоторая ненулевая сила Fn, направленная внутрь объема газа.
Очевидно, что сила FII пропорциональна концентрации молекул газа: FII ~ n0. Кроме того, число молекул в пристеночном слое тоже пропорционально n0. Значит суммарная сила, действующая на все молекулы, находящиеся у стенки и направленная внутрь газа, пропорциональна n02. Картина такова, как будто к давлению р, оказываемому на газ со стороны стенок сосуда, добавляется некоторая величина рi, называемая внутренним давлением газа и равная этой силе, отнесенной к единице площади. Поэтому рi ~ n02 ~ 1/Vμ2
Уравнение (2) можно переписать теперь в виде:
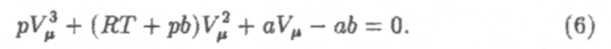
| В зависимости от значений р и T число вещественных корней уравнения (6) равно одному или трем. Это наглядно показывают графики зависимости р от V при различных фиксированных Т — изотермы (рис. 7). |

где а — константа, разная для разных газов и называемая поправкой Ван-дер-Ваалъса на межмолекулярное взаимодействие.
Итак,
следствием взаимного притяжения молекул является дополнительное (внутреннее) давление, которое обратно пропорционально квадрату объема газа.
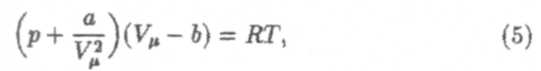
причем считаем, что постоянные a и b зависят только от природы газа
Если υ молей газа занимают объем V, то молярный объем этого газа Vμ = V/υ. Подстановка в (5) дает уравнение Ван-дер-Ваальса для произвольного количества газа:
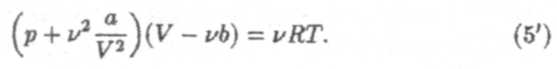
|
Уравнения (5) и (5') применимы при следующих условиях:
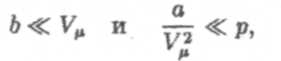
|
то есть, когда плотность газа не слишком велика. Лля очень плотных газов (6 ~ VM) уравнение Ван-дер-Ваальса хотя и расходится с опытом количественно, но качественно остается верным (в этом его преимущество перед уравнением Менделеева-Клапейрона (1)). Кроме того, при его выводе использованы совершенно ясные физические предположения. Поэтому можно применять это уравнение для качественного описания поведения реальных газов.
Дата добавления: 2015-08-11; просмотров: 1515;
