Ядерний спін
Фізичні основи спектроскопії ЯМР
Відомо, що всі мікрочастинки, такі як нуклони, що формують атомне ядро, є квантовими частками, тобто такими, що можуть мати лише певний набір енергетичних рівнів, що визначаються їхніми квантовими числами. Перехід з одного енергетичного рівня на інший супроводжується поглинанням або випромінюванням кванта енергії. Таким чином і сам атом є квантовою частинкою, для якої можливий цілком певний набір енергетичних станів. Кількість цих станів визначається квантовими числами. Більшість квантових чисел описує електронну будову атомів – кількість можливих електронних оболонок, їхню форму, тощо. Але одне з квантових чисел – спінове квантове число є приналежністю саме атомного ядра. Воно пов’язане з обертальним рухом нуклонів у ядрі і визначає поведінку ядра при його взаємодії з зовнішніми постійними і змінними магнітними полями. Ядра всіх атомів характеризуються спіновим квантовим числом, I, що може приймати нульове значення, а також позитивні значення, кратні ½. У випадку, якщо I=0, ядро не має спіну, тобто його сумарний магнітний момент дорівнює нулю. Це відбувається у випадку, коли і атомний номер і атомна маса ядра парні. Такі ядра не здатні змінювати свій енергетичний стан під впливом зовнішніх магнітних полів, тобто їх неможливо вивчати методами, що базуються на поглинанні ядрами електромагнітної енергії. Відомо, що більшість синтезованих до теперішнього часту хімічних сполук містять атоми вуглецю. Це не тільки органічні сполуки, а й більшість комплексних сполук. З погляду хіміка неприємним є те, що найцікавіше для вивчення цих сполук ядро, 12С, має нульовий спін, оскільки в нього і атомна маса і атомний номер парні. Це дещо звужує можливості застосування радіоспектроскопії для вивчення структури хімічних сполук. Але у переважної більшості хімічних елементів (і вуглецю також) є принаймні один ізотоп з ненульовим спіном, придатний для вивчення методом ЯМР (Табл. 1.1)
Таблиця 1.1Властивості найважливіших ядер зі спіном 1/2
| Ізотоп | Природний вміст ( %) | ЯМР Частота (МГц) | Відносна чутливість |
| 1H | 99.98 | 400.0 | 1.0 |
| 3H | 426.7 | 1.2* | |
| 13C | 1.11 | 100.6 | 1.76 x 10-4 |
| 15N | 0.37 | 40.5 | 3.85 x 10-6 |
| 19F | 100.00 | 376.3 | 0.83 |
| 29Si | 4.7 | 79.5 | 3.69 x 10-4 |
| 31p | 100.00 | 161.9 | 6.63 x 10-2 |
| 77Se | 7.58 | 76.3 | 5.25 x 10-4 |
| 103Rh | 100.00 | 12.6 | 3.11 x l0-5 |
| 113Cd | 12.16 | 88.7 | 1.33 x l0-3 |
| 119Sn | 8.58 | 149.1 | 4.44 x l0-3 |
| 183W | 14.40 | 16.6 | 1.03 x 10-5 |
| 195pt | 33.80 | 86.0 | 3.36 x 10-3 |
| 207pb | 22.60 | 83.7 | 2.07 x 10-3 |
Частоти наведені для спектрометра на 400 Гц (магніт 9.4 T); чутливості дані відносно протонів.
Вони включають множники чутливості ядра і його природного вмісту. Властивості квадрупольних ядер дані нижче в Таблиці 2.3.
*За умови 100% 3H збагачення
Тому все ж спектроскопію ЯМР на ядрах вуглецю можна застосовувати, хоча і з значно меншою чутливістю, ніж це б нам хотілося. Деякою розрадою є те, що теж дуже важливе для хіміків ядро, протон, є найбільш чутливим в ЯМР. Наявність ядерного спіну є визначальною для явища ЯМР.
Магнітні властивості атомних ядер можна собі уявити, якщо вважати ядра твердими утвореннями певної форми, поверхня яких має надпровідні властивості. На цій поверхні рівномірно розподілений позитивний заряд, що є характерним для даного ядра. Ядро весь час обертається вздовж певної осі. Таким чином, і заряд, що зосереджений на поверхні ядра також обертається. Це еквівалентно руху зарядів у мікроскопічному завитку провідника, а з фізики відомо, що це приводить до виникненні навколо ядра магнітного поля певної конфігурації. Як і кожна матеріальна частка, ядро що обертається, має механічний момент Р. Оскільки магнітні властивості ядра також зумовлені обертанням його зарядженої поверхні, то магнітний момент ядра m пов’язаний з його механічним моментом. Для зв’язку магнітного та механічного моментів ядра справедливим є рівняння:
m = gP (1.1)
де множник g називається гіромагнітним відношенням.

Рис.1.1.У ядрі, що має заряд, при обертанні виникає магнітний момент μ
Гіромагнітне відношення є сталою величиною для ядер даного типу і показує, наскільки великим є магнітний момент ядра. Як механічний момент ядра, так і його магнітний момент - величини векторні. Тому вони характеризуються не тільки величиною, а й напрямком. За відсутності зовнішнього магнітного поля енергетичні стани ядра є однаковими (виродженими), тому орієнтація обертального руху кожного ядра є цілком довільною та незалежною від орієнтації інших магнітних ядер зразка. Якщо внести зразок, що містить магнітні ядра, в зовнішнє магнітне поле (позначимо щільність його магнітного потоку Во), то ядра, завдяки своїм магнітним властивостям, будуть орієнтуватися лише цілком певним чином. Тут є аналогія з мікроскопічними стрілками компаса, що внесені у магнітне поле. Всі такі стрілки розташуються вздовж силових ліній магнітного поля, причому Північний полюс стрілок буде спрямованим до Південного полюсу зовнішнього магнітного поля. Але, на відміну від стрілок компаса, для яких існує лише одна енергетично вигідна орієнтація, для мікроскопічних магнітних моментів атомних ядер відносно цього поля можуть реалізуватися декілька дискретних орієнтацій. Це пов'язане з тим, що спінове квантове число ядра визначає декілька можливих енергетичних станів ядра. Для спіну з магнітним квантовим числом I можливе існування 2I+1 таких станів. Тому для ядер зі спіном 1/2 , таких як протони, можливе існування двох станів, які позначаються +1/2 і -1/2. Для ядер з I=1, наприклад, для дейтерію, можливими є спінові стани +1,0 і -1 (Рис. 1.2).
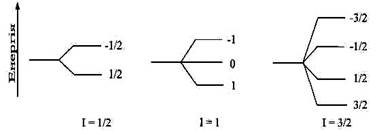
Рис. 1.2.Ядро з магнітним квантовим числом I може приймати 2І + 1 орієнтацій відносно прикладеного статичного магнітного поля Bo. Для ядра зі спіном '/2, моделлю поводження ядра служить мікроскопічна магнітна пластинка, що має дві можливі орієнтації, a і b
Для ядер зі спіном ½, де існує всього два спінових стани, їх часто позначають a і b, причому приймають, що перший з них має меншу енергію. Найлегше спінові стани ядра зі спіном ½ уявити собі, якщо вважати, що ядро не є ідеальною сферою, а схоже за формою на sp-орбіталь (асиметрична гантель). У зовнішньому магнітному полі таке ядро своєю віссю завжди орієнтується вздовж силових ліній поля, оскільки саме така орієнтація відповідає мінімуму енергії системи, але для нього можливі дві нерівноцінні орієнтації, що дещо відрізняються за енергією. В одній з них до Північного полюсу магніту спрямований більш об’ємний кінець гантелі, а в іншій – менш об’ємний. Слід також врахувати, що точна орієнтація ядра вздовж поля заборонена принципом невизначеності Гейзенберга, оскільки в цьому випадку і локалізація ядра і його енергія були б цілком визначеними. Тому магнітні моменти ядер орієнтуються не точно вздовж поля, а під певним кутом до нього. В цьому випадку зберігається невизначеність локалізації ядра. Вплив статичного поля на магнітний момент ядра можна змоделювати за допомогою класичної механіки. Поле змушує магнітний момент прецесувати довкола нього. Внаслідок цього вектор магнітного моменту ядра робить кругові рухи навколо напрямку Во (Рис. 1.3.). Якщо вважати ядро схожим на асиметричну гантель, то в одному спіновому стані більш об’ємний кінець гантелі прецесуватиме вздовж поля, а в іншому – проти поля. Такий рух будемо надалі називати Ларморовою прецесією. Він аналогічний до руху гіроскопа в гравітаційному полі Землі, коли гіроскоп обертається навколо своєї осі і одночасно прецесує навколо напрямку гравітаційного поля. Прецесія описується кутовою швидкістю (w радіан/с або n Гц):
w = gBo рад/c (1.2)
n = -gBo/2p = -gBo (1.3)
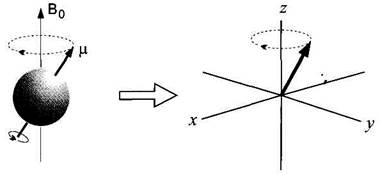
Рис. 1.3.Статичне магнітне поле, що прикладене до ядра, є причиною його прецесії. Швидкість прецесії залежить від сили поля і гіромагнітного відношення ядра. Поле прикладене уздовж осі z Декартової системи координат, а рух ядра представлений як рух вектора по поверхні конусу.
і відома як Ларморова частота ядра. Напрямок руху визначається знаком g. Він може відбуватися за годинниковою стрілкою або проти неї, однак завжди в один бік для всіх ядер даного типу. Ядерний магнітний резонанс відбувається тоді, коли під впливом зовнішніх факторів ядра змінюють спіновий стан, що супроводжується поглинанням кванта енергії. Енергія може поглинатися тільки за рахунок впливу електромагнітного поля, частота якого відповідає частоті Ларморової прецесії ядер. Її можна знайти зі співвідношення:
DE = hn = hgBo/2p (1.4)
де h - стала Планка. Інакше кажучи, резонансна частота ядра дорівнює його Ларморовій частоті. Новітні спектрометри ЯМР високого розділення мають напруженість магнітного поля до 20 Т (Тесла), що для протонів відповідає резонансній частоті 900 Мгц. Для інших ядер у такому самому полі частота поглинання буде відмінною від протонів внаслідок її залежності від гіромагнітного відношення конкретного ядра. Загальновживаною є практика характеризувати прилади за тією частотою, що відповідає резонансу протонів. Так, наприклад, якщо використовується спектрометр на 400 МГц, то протони на ньому поглинають при 400 МГц, а ядра вуглецю-13 – при 100 МГц, оскільки gH/gC = 4. Формула (1.4) показує, що величина кванта енергії, що поглинається ядром, DE, є пропорційною до сили зовнішнього магнітного поля Bo. Зрозуміло, що чим більше енергії поглинається в експерименті ядерного магнітного резонансу, тим легше її зареєструвати. Отже чутливість експерименту зростає при використанні спектрометрів з більш потужними магнітами. Саме в цьому і є сенс використання якомога більш потужних магнітів, незважаючи на суттєве зростання ціни приладів.
При розгляді явища ЯМР найбільш часто вважають, що статичне магнітне поле розташовується вздовж осі z декартової системи координат. Тому ядра зі спіном ½, що прецесують у магнітному полі, мають компонент намагніченості уздовж цієї осі (поздовжня намагніченість) і в перпендикулярному напрямку, у площині х-у (поперечна намагніченість), Рис. 1.3.
Тепер розглянемо, як статичне магнітне поле впливає на реальний зразок хімічної речовини, що містить велику кількість однакових ядер зі спіном ½. Така ситуація реалізується, наприклад, для зразку хлороформу. Як вказувалося раніше, орієнтація спінів у напрямку прикладеного поля, a, має трохи нижчу енергію, ніж орієнтація b. Різницю енергій спінових станів можна позначити як DE. Якщо згадати модель асиметричної гантелі, то можна вважати, що орієнтації a відповідає таке розташування ядра, коли навколо напряму до Північного полюсу магніту прецесує більший кінець гантелі. Для ядер, що знаходяться у стані b ситуація зворотна. Зразок знаходиться у стані теплової рівноваги. Це означає, що існує певна рівновага між всіма можливими енергетичними станами ядер. Вірогідність перебування ядра на кожному з енергетичних рівнів можна охарактеризувати фізичним параметром, що зветься населеністю рівня. Населеність – це частка, або відсоток ядер, що перебувають на кожному з енергетичних рівнів. Чим більш енергетично вигідним є рівень, тим більше ядер перебуватиме на ньому. Кількісно населеності рівнів можна обчислити за допомогою статистичного розподілу Больцмана. У згоді з ним, для спіну ½ надлишок населеності більш енергетично вигідного рівня становитиме:
Na/Nb = eDE/RT (1.5)
де Na, Nb – відповідає кількості ядер з певною спіновою орієнтацією, R – універсальна газова стала, а Т – абсолютна температура у Кельвінах. З формули витікає, що відношення населеностей енергетичних рівнів (спінових станів) визначається різницею їхньої енергії, а вона, в свою чергу, як це ми бачили раніше, є пропорційною до напруженості зовнішнього магнітного поля. Отже сенс використання потужних магнітів полягає також і в збільшенні різниці населеностей енергетичних рівнів, що зумовлює підвищення чутливості експерименту. Але, однаково, різниця енергії між рівнями є досить малою, тому і різниця в населеностях рівнів також не дуже істотна і становить близько 10001:10000 для максимально досяжних магнітних полів. Саме внаслідок малої різниці населеностей енергетичних рівнів метод ЯМР малочутливий у порівнянні з такими спектроскопічними методами як ІЧ або УФ, де різниця енергії між основним і збудженим станом є значно більшою.
Якщо магнітний момент кожного з ядер зразка представити у вигляді вектора, то населеності ядерних спінів будуть визначатися як сукупність векторів окремих спінів, що рівномірно розподілені по конусам прецесії навколо напрямку прикладеного зовнішнього магнітного поля, що мають спільну вершину. Якщо розглянути таку систему векторів, можна побачити, що більшість векторів в ній мають вектори-антиподи, що спрямовані в протилежний бік. Векторна сума таких пар векторів буде дорівнювати нулю. Сумарна намагніченість зразка формується за рахунок лише тих векторів, що не мають антиподів. Їхня векторна сума утворює вектор намагніченості Мо вздовж зовнішнього поля (Рис. 1.4). Таким чином, сумарна намагніченість зразка з'являється через різницю населеностей енергетичних рівнів ядра. Оскільки вектори окремих ядер рівномірно розподілені по конусу прецесії, то в зразку, що вміщений в зовнішнє магнітне поле, не виникає поперечної намагніченості в площині х-у (усереднена намагніченість у цій площині дорівнює нулю). Тому ми можемо спростити нашу картину намагніченості зразка в зовнішньому магнітному полі, замінивши безліч векторів намагніченості окремих ядер на один вектор намагніченості Мо, спрямований вздовж напрямку прикладеного магнітного поля, що підкоряється законам класичної механіки. Така спрощена векторна модель називається векторною моделлю Блоха на честь одного з основоположників ЯМР Фелікса Блоха або просто векторною моделлю ЯМР. Таким чином, при внесенні зразка, що містить магнітні ядра, у магнітне поле, виникає певна намагніченість, що описується вектором Мо.
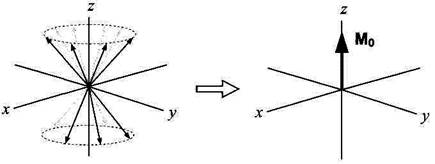
Рис. 1.4.У векторній моделі ЯМР безліч однакових спінів представлені як велика кількість векторів намагніченості, що розподілені рівномірно по поверхням двох конусів прецесії. Якщо знайти векторну суму всіх цих векторів, отримаємо сумарний вектор Мо, що спрямований уздовж осі +z. Він відповідає надлишку спінів у стані a.
Дата добавления: 2015-08-11; просмотров: 952;
