Сходимость числовых положительных рядов
Одной из ключевых задач теории числовых рядов является исследование ряда на сходимость. На практике в подавляющем большинстве примеров сумму ряда находить не требуется.Для установления сходимости (расходимости) ряда можно не пытаться найти сумму ряда. Для этого используются специальные признаки, по которым можно опрендлить является ли ряд сходящимся или наоборот расходящимся. Таких признаков сходимости существует несколько: необходимый признак сходимости ряда, признаки сравнения, признак Даламбера, признаки Коши и некоторые другие.
Когда какой признак применять? Это зависит от общего члена ряда 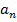 , образно говоря – от «начинки» ряда. Так, рассмотрим необходимое условие сходимости знакоположительного ряда
, образно говоря – от «начинки» ряда. Так, рассмотрим необходимое условие сходимости знакоположительного ряда
Определение. Если числовой ряд 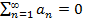 сходится, то предел его n-ого члена равен нулю:
сходится, то предел его n-ого члена равен нулю: 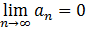
Почему признак называется необходимым? Потому-что, если общий член ряда стремится кнулю, то мы уже знаем на примере гармонического ряда, что это еще не значит, что ряд сходится. Или так: для того, чтобы ряд сходился, необходимо, чтобы его общий член стремился к нулю; но этого еще – не достаточно. Если общий член ряда стремится к нулю, то ряд может, как сходиться, так и расходиться! В таких случаях для решения примеров нужно использовать другие признаки, называемые достаточными признаками сходимости ряда.
Дата добавления: 2015-08-11; просмотров: 1191;
