Первый признак сравнения рядов.
Пусть 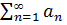 и
и 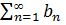 - два знакоположительных числовых ряда и выполняется неравенство
- два знакоположительных числовых ряда и выполняется неравенство
 для всех n = 1, 2, 3, ... Тогда из сходимости ряда
для всех n = 1, 2, 3, ... Тогда из сходимости ряда 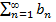 следует сходимость
следует сходимость 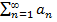 , а из расходимости ряда
, а из расходимости ряда 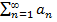 следует расходимость
следует расходимость 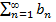 .
.
Первый признак сравнения используется очень часто и представляет собой очень мощный инструмент исследования числовых рядов на сходимость. Основную проблему представляет подбор подходящего ряда для сравнения. Ряд для сравнения обычно (но не всегда) выбирается так, что показатель степени его k-ого члена равен разности показателей степени числителя и знаменателя n-ого члена исследуемого числового ряда. К примеру, пусть  , разность показателей степени числителя и знаменателя равна 2 – 3 = -1, поэтому, для сравнения выбираем ряд с n-ым членом
, разность показателей степени числителя и знаменателя равна 2 – 3 = -1, поэтому, для сравнения выбираем ряд с n-ым членом 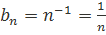 , то есть, гармонический ряд. Рассмотрим несколько примеров.
, то есть, гармонический ряд. Рассмотрим несколько примеров.
Пример.1
Исследуйте числовой ряд  на сходимость.
на сходимость.
Решение.
Необходимое условие сходимости числового ряда выполняется, так как 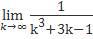 . Очевидно выполнение неравенства
. Очевидно выполнение неравенства  для любого натурального значения k. Ряд сходится, так как обобщенно гармонический ряд
для любого натурального значения k. Ряд сходится, так как обобщенно гармонический ряд 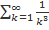 является сходящимся для
является сходящимся для 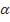 > 1. Таким образом, первый признак сравнения рядов позволяет констатировать сходимость исходного числового ряда.
> 1. Таким образом, первый признак сравнения рядов позволяет констатировать сходимость исходного числового ряда.
Пример 2.
Определите сходимость или расходимость числового ряда 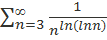 .
.
Решение. Проверим необходимое условие сходимости ряда
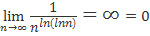 , следовательно, необходимое условие сходимости числового ряда выполнено. Какой ряд выбрать для сравнения? Напрашивается числовой ряд
, следовательно, необходимое условие сходимости числового ряда выполнено. Какой ряд выбрать для сравнения? Напрашивается числовой ряд 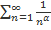 , а чтобы определиться с
, а чтобы определиться с 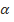 внимательно исследуем числовую последовательность ln(lnn) n=3,4,4,…. Члены числовой последовательности ln(ln3), ln(ln4), ln(ln5), …возрастают к бесконечности. Таким образом, начиная с некоторого номера N (а именно, с N = 1619), члены этой последовательности будут больше 2. Начиная с этого номера N, справедливо неравенство .
внимательно исследуем числовую последовательность ln(lnn) n=3,4,4,…. Члены числовой последовательности ln(ln3), ln(ln4), ln(ln5), …возрастают к бесконечности. Таким образом, начиная с некоторого номера N (а именно, с N = 1619), члены этой последовательности будут больше 2. Начиная с этого номера N, справедливо неравенство . 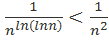 Числовой ряд
Числовой ряд 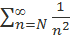 сходится в силу первого свойства сходящихся рядов, так как получается из сходящегося ряда отбрасыванием первых N – 1 члена. Таким образом, по первому признаку сравнения сходящимся является ряд
сходится в силу первого свойства сходящихся рядов, так как получается из сходящегося ряда отбрасыванием первых N – 1 члена. Таким образом, по первому признаку сравнения сходящимся является ряд 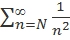 , а в силу первого свойства сходящихся числовых рядов сходится будет и ряд
, а в силу первого свойства сходящихся числовых рядов сходится будет и ряд 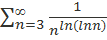 .
.
Дата добавления: 2015-08-11; просмотров: 1099;
