Суммой сходящегося числового ряда.
В качестве примера расходящегося ряда можно привести сумму геометрической прогрессии со знаменателем большем, чем единица1+2+4+….+ 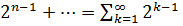 определяется выражением
определяется выражением 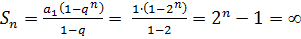 ,
,
Еще одним примером расходящегося числового ряда является сумма вида 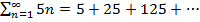 . В этом случае n–ая частичная сумма может быть вычислена как
. В этом случае n–ая частичная сумма может быть вычислена как  . Предел частичных сумм бесконечен .
. Предел частичных сумм бесконечен .
Сумма вида 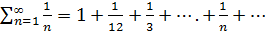 называется гармоническим числовым рядом.
называется гармоническим числовым рядом.
Сумма вида 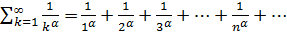 где
где  – некоторое действительное число, называется обобщенно гармоническим числовым рядом.
– некоторое действительное число, называется обобщенно гармоническим числовым рядом.
Приведенных определений достаточно для обоснования следующих очень часто используемых утверждений, рекомендуем их запомнить.
Докажем, что гармонический ряд расходится.
Запишем гармонический ряд в развернутом виде:
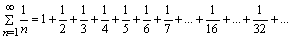
и наряду с ним рассмотрим ряд с меньшими членами, который получен из гармонического заменой  на
на  ;
;  ,
,  ,
,  на
на  ;
; 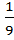 ,
, 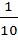 , …,
, …, 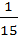 на
на 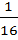 и т.д.
и т.д.
Ясно, что члены этого ряда уменьшились по сравнению с гармоническим рядом, а это дает нам возможность найти частичные суммы этого ряда либо доказать, что ряд расходится. Действитель-но, получен ряд вида:
1+  +
+  +
+ 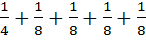 и.т.д., сложив в этом ряде выделенные группы, получим бесконечный ряд из сумм
и.т.д., сложив в этом ряде выделенные группы, получим бесконечный ряд из сумм  . Значит ряд расходится.
. Значит ряд расходится.
Обобщенный гармонический ряд 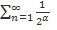 сходится при
сходится при 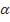 > 1 и расходится при
> 1 и расходится при 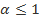 .
.
Дата добавления: 2015-08-11; просмотров: 1012;
