Основные определения и понятия.

Пусть мы имеем числовую последовательность 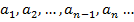где

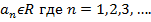
Приведем пример числовой последовательности: .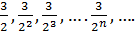

Числовой ряд – это сумма членов числовой последовательности вида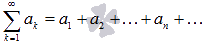

В качестве примера числового ряда можно привести сумму бесконечно убывающей геометрической прогрессии со знаменателем q = -0.5: 8-4+2-1+ .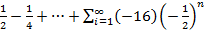

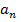называют общим членом числового ряда. Здесь 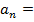(-16)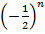

. Частичная сумма числового ряда – это сумма вида 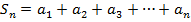, где n – некоторое натуральное число. называют также n-ой частичной суммой числового ряда.

К примеру, четвертая частичная сумма ряда 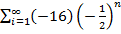есть 8-4+2-1=5.

Частичные суммы 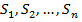образуют бесконечную последовательность частичных сумм числового ряда.

Для нашего ряда n –ая частичная сумма находится по формуле суммы первых n членов геометрической прогрессии , то есть, будем иметь следующую последовательность частичных сумм: 8,4,6,5….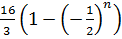

Числовой ряд 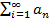называется сходящимся, если существует конечный предел последовательности частичных сумм 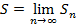. Если предел последовательности частичных сумм числового ряда не существует или бесконечен, то ряд 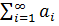называется расходящимся.