Следствие.

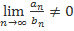Если и , то из сходимости одного ряда следует сходимость другого, а из расходимости следует расходимость.

Исследуем ряд 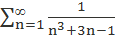на сходимость с помощью второго признака сравнения. В качестве ряда 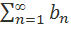возьмем сходящийся ряд 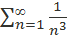. Найдем предел отношения n-ых членов числовых рядов:
=

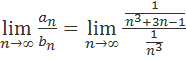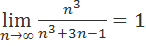
Таким образом, по второму признаку сравнения из сходимости числового ряда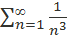

следует сходимость исходного ряда.

Пример 3.

Исследовать на сходимость числовой ряд .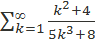

Решение.

Проверим необходимое условие сходимости ряда 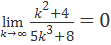. Условие выполнено. Для применения второго признака сравнения возьмем гармонический ряд 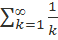. Найдем предел отношения k-ых членов:
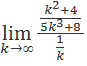= Следовательно, из расходимости гармонического ряда следует расходимость исходного ряда по второму признаку сравнения.

Для информации приведем третий признак сравнения рядов.