Третий признак сравнения.

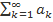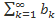Пусть и - знакоположительные числовые ряды. Если с некоторого номера N выполняется условие 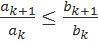, то из сходимости ряда 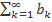следует сходимость 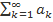, а из расходимости ряда 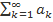следует расходимость .

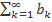Теорема (признак Даламбера). Если в ряде с положительными членами 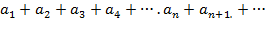отношение n+1-го члена ряда n -му при n 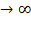имеет конечный предел q, т.е.

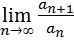,=q, то: - ряд сходится в случае при q<1, - ряд расходится в случае q>1.
В случаях, когда предел не существует или он равен единице, ответа на вопрос о сходимости или расходимости числового ряда теорема не дает. Необходимо провести дополнительное исследование.