Радикальный признак Коши.

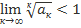Пусть - знакоположительный числовой ряд. Если , то числовой ряд сходится, если 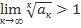, то ряд расходится.

Замечание. Радикальный признак Коши справедлив, если предел бесконечен, то есть, если 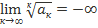, то ряд сходится, если 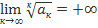, то ряд расходится.

Если 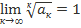, то радикальный признак Коши не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование.

Обычно достаточно легко разглядеть случаи, когда лучше всего использовать радикальный признак Коши. Характерным является случай, когда общий член числового ряда представляет собой показательно степенное выражение. Рассмотрим несколько примеров.

Пример1.

Исследовать знакоположительный числовой ряд 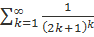на сходимость с помощью радикального признака Коши.

Решение.

Необходимое условие сходимости ряда выполнено, так как 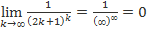. По

радикальному признаку Коши получаем .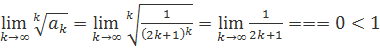

Следовательно, ряд сходится.

Приме 2 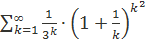.Сходится ли числовой ряд .

Решение.

Воспользуемся радикальным признаком Коши 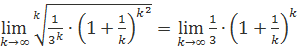, = <1, следовательно, числовой ряд сходится.