Графическое представление вариационного ряда.

1. Центральную тенденцию выборки позволяют оценить такие статистические характеристики, как среднее арифметическое значение, мода, медиана.

Наиболее просто получаемой мерой центральной тенденции является мода. Мода – это такое значение в множестве наблюдений, которое встречается наиболее часто. В случае, когда все значения в группе встречаются одинаково часто, считают, что эта группа не имеет моды. Когда два соседних значения в ранжированном ряду имеют одинаковую частоту и они больше частоты любого другого значения, мода есть среднее этих двух значений. Если два несмежных значения в группе имеют равные частоты, и они больше частот любого значения, то существуют две моды; в таком случае группа измерений или оценок является бимодальной.

Наибольшей модой в группе называется единственное значение, которое удовлетворяет определению моды. Однако во всей группе может быть несколько меньших мод. Эти меньшие моды представляют собой локальные вершины распределения частот.

Медиана (Me) – середина ранжированного ряда результатов измерений. Если данные содержат четное число различных значений, то медиана есть точка, лежащая посередине между двумя центральными значениями, когда они упорядочены.

Среднее арифметическое значение 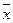для неупорядоченного ряда измерений вычисляют по формуле:

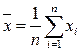, (2.2)

где .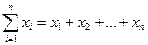

Каждая из выше вычисленных мер центра является наиболее пригодной для использования в определенных условиях.

Мода вычисляется наиболее просто – ее можно определить на глаз. Более того, для очень больших групп данных это достаточно стабильная мера центра распределения.

Медиана занимает промежуточное положение между модой и средним с точки зрения ее вычисления. Эта мера получается особенно легко в случае ранжированных данных. Ранжированием называют расстановку результатов измерений в порядке возрастания или убывания.

Среднее арифметическое значение рассчитывается в основном в целях проведения арифметических операций.

На величину среднего влияют значения всех результатов. Медиана и мода не требуют для определения всех значений. На величину среднего особенно влияют результаты, которые называют “выбросами”, т.е. данные, находящиеся далеко от центра группы оценок.

Вычисление моды, медианы или среднего – чисто техническая процедура. Однако выбор из этих трех мер и их интерпретация зачастую требуют определенного размышления. В процессе выбора следует установить следующее:

– в малых группах мода может быть совершенно нестабильной;

– на медиану не влияют величины “больших” и “малых” значений;

– на величину среднего влияет каждое значение;

– некоторые множества данных не имеют центральной тенденции, что часто вводит в заблуждение при вычислении только одной меры центральной тенденции;

– когда считают, что группа данных является выборкой из большой симметричной группы, среднее выборки, вероятно, ближе к центру большой группы, чем медиана и мода.

Все средние характеристики дают общую характеристику ряда результатов измерений. На практике нас часто интересует, как сильно каждый результат отклоняется от среднего значения. Однако легко можно представить, что две группы результатов измерений имеют одинаковые средние, но различные значения измерений.

Поэтому средние характеристики всегда необходимо дополнять показателями вариации, или колеблемости.

2. К характеристикам вариации, или колеблемости, результатов измерений относят размах варьирования, дисперсию, среднее квадратическое отклонение, коэффициент вариации, стандартную ошибку средней арифметической.

Самой простой характеристикой вариации является размах варьирования. Его определяют как разность между наибольшим и наименьшим результатами измерений. Однако он улавливает только крайние отклонения, но не отражает отклонений всех результатов.

Чтобы дать обобщающую характеристику, можно вычислить отклонения от среднего результата. Сумма этих отклонений всегда равна 0. Чтобы избежать этого, значения каждого отклонения возводят в квадрат. Значение 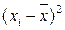делает отклонения от средней более явственными. Получившуюся сумму 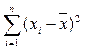называют суммой квадратов отклонений. Разделив эту сумму на число измерений, получают средний квадрат отклонений, или дисперсию. Она обозначается s² и вычисляется по формуле:

.

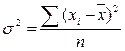Если число измерений не более 30, т.е. n ≤ 30, используется формула:

.

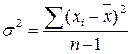Величина n – 1 = k называется числом степеней свободы, под которым подразумевается число свободно варьирующих членов совокупности. Установлено, что при вычислении показателей вариации один член эмпирической совокупности всегда не имеет степени свободы.

Эти формулы применяются, когда результаты представлены неупорядоченной (обычной) выборкой.

Из характеристик колеблемости наиболее часто используется среднее квадратическое отклонение, которое определяется как положительное значение корня квадратного из значения дисперсии, т.е.:

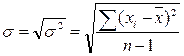. (2.5)

Среднее квадратическое отклонение или стандартное отклонение характеризует степень отклонения результатов от среднего значения в абсолютных единицах и имеет те же единицы измерения, что и результаты измерения.

Однако для сравнения колеблемости двух и более совокупностей, имеющих различные единицы измерения, эта характеристика не пригодна.

Коэффициент вариации определяется как отношение среднего квадратического отклонения к среднему арифметическому, выраженное в процентах. Вычисляется он по формуле:

.

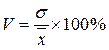В спортивной практике колеблемость результатов измерений в зависимости от величины коэффициента вариации считают небольшой
(0 – 10 %), средней (11 – 20 %) и большой (V > 20 %).

Коэффициент вариации имеет важное значение в спортивной метрологии, т. к., будучи величиной относительной (измеряется в процентах), позволяет сравнивать между собой колеблемость результатов измерений, имеющих различные единицы измерения. Коэффициент вариации можно использовать лишь в том случае, если измерения выполнены в шкале отношений.

3. Выборки большого объема разбивают на интервалы. В простейшем случае их может быть два. Например, когда необходимо отобрать худших или лучших спортсменов. Однако, для получения достаточно точных результатов число интервалов (его обозначают буквой k) должно быть больше. В зависимости от объема выборки k устанавливают, придерживаясь формулы американского статистика Стерджесса

,

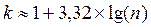где n – объём выборки.Тогда величина, или шаг интервала, определяется:

,

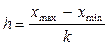где 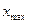– максимальный результат измерений в выборке, 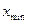– минимальный результат.

Используя полученный данные, определяют границы интервалов, а затем частоты интервалов. Частота интервала – количество значений числового ряда, которые попали в данный интервал. Распределение, составленное из частот, в статистике называют вариационным рядом.

Анализ вариационных рядов упрощается при графическом представлении. Основные графики вариационного ряда: полигон распределения – график строится в прямоугольной системе координат. Середины интервалов откладываются на оси абсцисс, частоты – на оси ординат. Гистограмма распределения – график строится аналогично полигону распределения, однако на оси абсцисс откладываются не точки (середины интервалов), а отрезки, отображающие интервал, и вместо ординат, соответствующих частотам или частостям отдельных вариантов, строят прямоугольники с высотой, пропорциональной частотам интервалов.

Контрольные вопросы для самопроверки:

1. Как вычисляется среднее арифметическое значение выборки?

2. Дайте определения моды и медианы.

3. Исходя из чего выбирается мера центральной тенденции?

4. Как вычисляется и что показывают дисперсия и среднее квадратическое отклонение?

5. Как вычисляется и что показывает стандартная ошибка среднего арифметического?

6. Как вычисляется и для чего используется коэффициент вариации?

7. Что такое вариационный ряд результатов измерения?

8. Как строятся полигон и гистограмма распределения?

Литература:

1. Основы математической статистики. Уч. пособие для ин-тов физической культуры (под общ. ред. В.С. Иванова). – М.: Физкультура и спорт, 1990. – С. 12 – 38.

2. Рукавицына С.Л., Волков Ю.О., Солтанович Л.Л. Спортивная метрология. Проверка эффективности методики тренировки с применением методов математической статистики. Практикум для студентов БГУФК. – Минск: БГУФК, 2006. – С. 22 – 29.

3. Гинзбург Г.И., Киселев В.Г. Расчетно-графические работы по спортивной метрологии. – Минск: БГОИФК, 1984. – С. 6 – 10.