Точность измерений.
1. Измерением называют установление соответствия между изучаемыми явлениями, с одной стороны, и числами, с другой.
Одним из вопросов, составляющих основы теории измерений, является вопрос о шкалах измерений.
В физической культуре и спорте используются четыре шкалы.
Шкала наименований (номинальная шкала). Это самая простая из всех шкал. В ней числа играют роль ярлыков и служат для обнаружения и различения изучаемых объектов (например, нумерация игроков футбольной команды). Числа, составляющие шкалу наименований, можно менять местами. В этой шкале нет отношений типа “больше-меньше”, поэтому некоторые полагают, что применение шкалы наименований не стоит считать измерением. При использовании шкалы наименований могут проводиться только некоторые математические операции. Ее числа нельзя складывать или вычитать. Но можно подсчитывать, сколько раз (как часто) встречается то или иное число.
Шкала порядка. В такой шкале составляющие ее числа упорядочены по рангам (занимаемым местам), но интервалы между ними точно измерить нельзя. Есть виды спорта, где результат спортсмена определяется только местом, занятым на соревнованиях (например, единоборства). После таких соревнований ясно только, кто из спортсменов сильнее, а кто слабее, но насколько – сказать нельзя. Есть, например, три спортсмена, занявшие соответственно, первое, второе и третье места. При этом второй спортсмен может быть почти равен первому, а может быть существенно слабее его и быть почти одинаковым с третьим. Места, занимаемые в шкале порядка, называют рангами, а сама шкала называется ранговой или неметрической. К рангам шкалы можно применять большее число математических операций, чем к числам шкалы наименований. Можно определить характер неравенства в виде суждений: “больше-меньше”, “лучше-хуже” и т.п. С помощью шкал порядка можно измерять качественные, не имеющие строгой количественной меры, показатели. Особенно широко эти шкалы используются в гуманитарных науках: педагогике, психологии, социологии.
Шкала интервалов. Это такая шкала, в которой числа не только упорядочены по рангам, но и разделены определенными интервалами. Особенность ее состоит в том, что нулевая точка выбирается произвольно. Примерами могут быть календарное время (начало летоисчисления в различных календарях устанавливалось по разным причинам), суставной угол (угол в локтевом суставе при полном разгибании предплечья может приниматься равным либо нулю, либо 1800), температура, потенциальная энергия поля и др. По шкале интервалов можно определять не только отношения “больше-меньше”, но и отвечать на вопрос “на сколько больше?”, но нельзя утверждать, что одно значение измеряемой величины во столько-то раз больше другого.
Шкала отношений. Эта шкала отличается от шкалы интервалов только тем, что в ней строго определено положение нулевой точки. В спорте по шкале отношений измеряют и те величины, которые образуются как разности чисел, отсчитанных по шкале интервалов. Так, календарное время отсчитывается по шкале интервалов, а интервалы времени – по шкале отношений. Если ограничиться только применением шкал отношений, то можно дать более узкое определение измерению: измерить какую-либо величину – значит найти опытным путем ее отношение к соответствующей единице измерения. Шкала отношений не накладывает никаких ограничений на математический аппарат, используемый для обработки результатов наблюдений.
2. Чтобы результаты разных измерений можно было сравнить друг с другом, их выражают в одних и тех же единицах. В 1960 году на Международной генеральной конференции по мерам и весам была принята Международная система единиц, получившая сокращенное название СИ (от начальных букв слов System International). В настоящее время установлено предпочтительное применение этой системы во всех областях науки и техники, в народном хозяйстве, а также при преподавании.
СИ в настоящее время включает семь независимых друг от друга основных единиц (см. табл. 1).
Из указанных основных единиц в качестве производных выводят единицы остальных физических величин. Производные единицы определяются на основе формул, связывающих между собой физические величины. Например, единица длины (метр) и единица времени (секунда) – основные единицы, а единица скорости (метр в секунду) – производная.
Кроме основных, в СИ выделены две дополнительные единицы: радиан – единица плоского угла и стерадиан – единица телесного угла (угла в пространстве).
Таблица 1
Основные единицы СИ
| Единицы | ||||
| Величина | Размер- ность | Название | Обозначение | |
| Русское | Междунар. | |||
| Длина | l | Метр | м | m |
| Масса | m | Килограмм | кг | kg |
| Время | t | Секунда | с | s |
| Сила электрического тока | I | Ампер | А | A |
| Температура | Q | Кельвин | К | K |
| Количество вещества | N | Моль | моль | mol |
| Сила света | g | Кандела | кд | cd |
Кроме того, различают кратные единицы, образованные с помощью увеличивающих приставок кило-, мега- и др. и дольные с приставками мили-, микро- и др.
Поскольку система СИ носит рекомендательный характер, часто используются внесистемные единицы, такие как часы, минуты, миллиметры ртутного столба, калории и др.
3. Никакое измерение не может быть выполнено абсолютно точно. Результат измерения неизбежно содержит погрешность, величина которой тем меньше, чем точнее метод измерения и измерительный прибор. Например, с помощью обычной линейки с миллиметровыми делениями нельзя измерить длину с точностью до 0,01 мм.
По происхождению различают основную и дополнительную погрешности.
Основная погрешность – это погрешность метода измерения или измерительного прибора, которая имеет место в нормальных условиях их применения.
Дополнительная погрешность – это погрешность измерительного прибора, вызванная отклонением условий его работы от нормальных. Понятно, что прибор, предназначенный для работы при комнатной температуре будет давать неточные показания, если пользоваться им летом на стадионе под палящим солнцем или зимой на морозе. Погрешности измерения могут возникать в том случае, когда напряжение электрической сети или батарейного источника питания ниже нормы или непостоянно по величине.
По способу выражения погрешности бывают абсолютные и относительные.
Величина DA = A – A0, равная разности между показанием измерительного прибора (A) и истинным значением измеряемой величины (A0), называется абсолютной погрешностью измерения. Она измеряется в тех же единицах, что и сама измеряемая величина.
На практике часто удобно пользоваться не абсолютной, а относительной погрешностью. Относительная погрешность измерения бывает двух видов – действительной и приведенной. Действительной относительной погрешностью называется отношение абсолютной погрешности к истинному значению измеряемой величины:
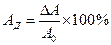 .
.
Приведенная относительная погрешность – это отношение абсолютной погрешности к максимально возможному значению измеряемой величины:
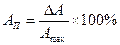 .
.
По изменчивости различают систематическую и случайную погрешности.
Систематической называется погрешность, величина которой не меняется от измерения к измерению. В силу этой своей особенности систематическая погрешность часто может быть предсказана заранее или, в крайнем случае, обнаружена и устранена по окончании процесса измерения.
Способ устранения систематической погрешности зависит в первую очередь от ее природы. Систематические погрешности измерения можно разделить на три группы:
1) погрешности известного происхождения и известной величины;
2) погрешности известного происхождения, но неизвестной величины;
3) погрешности неизвестного происхождения и неизвестной величины.
Самые безобидные – погрешности первой группы. Они легко устраняются путем введения соответствующих поправок в результат измерения.
Ко второй группе относятся, прежде всего, погрешности, связанные с несовершенством метода измерения и измерительной аппаратуры. Например, погрешность измерения физической работоспособности с помощью маски для забора выдыхаемого воздуха: маска затрудняет дыхание, и спортсмен закономерно демонстрирует физическую работоспособность, заниженную по сравнению с истинной, измеряемой без маски. Величину этой погрешности нельзя предсказать заранее: она зависит от индивидуальных способностей спортсмена и его самочувствия в момент исследования.
Другой пример систематической погрешности этой группы – погрешность, связанная с несовершенством аппаратуры, когда измерительный прибор заведомо завышает или занижает истинное значение измеряемой величины, но величина погрешности неизвестна.
Погрешности третьей группы наиболее опасны, их появление бывает связано как с несовершенством метода измерения, так и с особенностями объекта измерения – спортсмена.
Случайные погрешности возникают под действием разнообразных факторов, которые ни предсказать заранее, ни точно учесть не удается. Случайные погрешности принципиально не устранимы. Однако, воспользовавшись методами математической статистики, можно оценить величину случайной погрешности и учесть ее при интерпретации результатов измерения. Без статистической обработки результаты измерений не могут считаться достоверными.
Контрольные вопросы для самопроверки:
1. Что называют измерением?
2. Какие шкалы измерений используются в физической культуре и спорте. Охарактеризуйте каждую из них.
3. Единицы измерений системы СИ. Основные, дополнительные, производные, кратные, дольные, внесистемные единицы.
4. Основная и дополнительная погрешности.
5. Абсолютная и относительная погрешности.
6. Систематическая и случайная погрешности.
Литература:
1. Годик М.А. Спортивная метрология. Учебник для ин-тов физической культуры. – М.: Физкультура и спорт, 1988. – С. 9 – 16.
2. Спортивная метрология. Учебник для ин-тов физической культуры (под общ. ред. В.М. Зациорского). – М.: Физкультура и спорт, 1982. – С. 10 – 18/
3. Смирнов Ю.И., Полевщиков М.М. Спортивная метрология: Учеб. для студ. пед. вузов. – М.: Издательский центр «Академия», 2000. – С. 17 – 29, 67 – 72.
4. Рукавицына С.Л., Волков Ю.О., Солтанович Л.Л. Спортивная метрология. Проверка эффективности методики тренировки с применением методов математической статистики. Практикум для студентов БГУФК. – Минск: БГУФК, 2006. – С. 9 – 14.
Дата добавления: 2015-07-22; просмотров: 1259;
