Проверка нормальности распределения с помощью критерия Шапиро и Уилка.

1. Правило трёх сигм заключается в том, что практически все результаты, составляющие нормально распределенную выборку, находятся в пределах 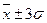. Это правило можно использовать при решении следующих важных задач:

1) Оценки нормальности распределения выборочных данных. Если результаты находятся примерно в пределах 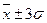и в области среднего арифметического результаты встречаются чаще, а вправо и влево от него – реже, то можно предположить, что результаты распределены нормально.

2) Выявление ошибочно полученных результатов. Если отдельные результаты отклоняются от среднего арифметического значения на величины, значительно превосходящие 3s, нужно проверить правильность полученных величин. Часто такие «выскакивающие» результаты могут появиться в результате неисправности прибора, ошибки в измерении и расчетах.

3) Оценка величины s. Если размах варьирования R=X_наиб - X_наим, разделить на 6, то мы получим грубо приближенное значение s.

2. Критерий W Шапиро и Уилка предназначен для проверки гипотезы о нормальном распределении генеральной совокупности, когда объём выборки мал (n ≤ 50). Процедура проверки следующая: выдвигается нулевая гипотеза о нормальном распределении генеральной совокупности. Рассчитывается наблюдаемое значение критерия Шапиро и Уилка W_набл и сравнивается с критическим значением W_крит, которое находится по таблице критических точек критерия Шапиро и Уилка в зависимости от объёма выборки и уровня значимости. Если W_набл ≥ W_крит, нулевая гипотеза о нормальном распределении результатов принимается; при W_набл < W_крит она отвергается.

Контрольные вопросы для самопроверки:

1. В чём заключается правило трёх сигм?

2. Практическое применение правила трёх сигм.

3. Какой критерий применяется для проверки нормальности распределения генеральной совокупности при малом объёме выборки?

4. Опишите процедуру проверки нормальности распределения.

Литература:

1. Основы математической статистики. Уч. пособие для ин-тов физической культуры (под общ. ред. В.С. Иванова). – М.: Физкультура и спорт, 1990. – С. 62 – 63, 110 – 112.

2. Рукавицына С.Л., Волков Ю.О., Солтанович Л.Л. Спортивная метрология. Проверка эффективности методики тренировки с применением методов математической статистики. Практикум для студентов БГУФК. – Минск: БГУФК, 2006. – С. 66 – 67.

3. Гинзбург Г.И., Киселев В.Г. Расчетно-графические работы по спортивной метрологии. – Минск: БГОИФК, 1984. – С. 21 – 22, 26 – 29.