Нормальный закон распределения.

1. Закон распределения результатов измерений – один из основных факторов, которым определяется выбор статистических методов обработки результатов измерений.

Закон распределения – закон, по которому распределяются вероятности непрерывных случайных величин. Получается из полигона распределения с бесконечно большим числом интервалов и наблюдений.

При анализе распределения результатов измерений всегда делают предположение о том распределении, которое имела бы выборка, если бы число измерений было очень большим (бесконечно большим). Такое распределение называют распределением генеральной совокупности или теоретическим, а распределение экспериментального ряда измерений – эмпирическим. При увеличении объёма выборки эмпирическое распределение будет приближаться к теоретическому.

2. Нормальный закон (закон Гаусса) распределения результатов измерений непрерывных величин наиболее часто встречается в спортивной практике.

Нормальное распределение описывается формулой, впервые предложенной английским математиком Муавром в 1733 году:

где p и e – математические константы (p = 3,141; e = 2,718); 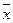и s – соответственно, среднее арифметическое и среднее квадратическое отклонение генеральной совокупности; x – результаты измерений; f(x) – так называемая функция плотности распределения.

Эта формула позволяет получить в виде графика кривую нормального распределения, которая симметрична относительно центра группирования.

Основные свойства кривой нормального распределения.

1) Кривая симметрична относительно среднего значения, которое является модой и медианой. При .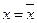

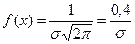2) При x ® ¥ f(x) ® 0.

3) Площадь, заключенная между кривой f(x) и осью x, равна единице.

4) Кривая имеет две точки перегиба при .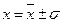

5) Изменение среднего арифметического значения не меняет форму кривой, а приводит лишь к сдвигу кривой вдоль оси x.

6) С увеличением s максимальная ордината кривой убывает, а сама кривая становится более пологой, при уменьшении s кривая становится более «островершинной». При любых значениях 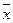и s площадь, ограниченная кривой и осью x, одинакова и равна единице.

В результате спортивной тренировки средняя арифметическая 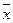должна улучшаться (в зависимости от вида спорта или увеличиваться, или уменьшаться), а стандартное отклонение s_г должно уменьшаться. С увеличением стабильности и устойчивости спортивных результатов, составляющих нормально распределенные выборки, кривая распределения становится более островершинной.

Контрольные вопросы для самопроверки:

1. Что такое закон распределения?

2. Для чего необходимо знать закон распределения случайной величины?

3. Теоретический и эмпирический закон распределения.

4. Сущность нормального закона распределения.

5. Свойства кривой нормального распределения.

Литература:

1. Основы математической статистики. Уч. пособие для ин-тов физической культуры (под общ. ред. В.С. Иванова). – М.: Физкультура и спорт, 1990. – С. 57 – 62.

2. Рукавицына С.Л., Волков Ю.О., Солтанович Л.Л. Спортивная метрология. Проверка эффективности методики тренировки с применением методов математической статистики. Практикум для студентов БГУФК. – Минск: БГУФК, 2006. – С. 63 – 65.

3. Гинзбург Г.И., Киселев В.Г. Расчетно-графические работы по спортивной метрологии. – Минск: БГОИФК, 1984. – С. 18 – 21.