Предмет математической статистики.

1. Теория вероятностей – раздел математики, который по известным вероятностям одних случайных величин определяет вероятности других случайных величин, взаимосвязанных с первыми.

Случайное событие – событие, которое может случиться во время проведения испытания, т.е. оно не закономерно, его нельзя достоверно предсказать заранее.

Случайная величина – такая величина, которая претерпевает случайные изменения от испытания к испытанию (от измерения к измерению). В зависимости от возможных значений случайная величина может быть дискретной или непрерывной. Например, при бросании игральной кости могут выпадать только целые значения (от 1 до 6) – это дискретная случайная величина; а время пробега спортсменом дистанции может изменяться плавно – это непрерывная случайная величина.

Вероятность – степень возможности появления случайного события в результате проведения испытания, которое может повториться бесконечное количество раз.

Существует статистическое и классическое определение вероятности. Рассмотрим статистическое определение.

Будем фиксировать число испытаний, в результате которых появилось событие А. Всего было проведено N испытаний. В результате этих испытаний событие А наступило n_N раз. Число n_N называется частотой события, а отношение n_N /N – частостью (относительной частотой) события А. (События в теории вероятностей принято обозначать заглавными латинскими буквами А, В, С, … .) Если мы будем увеличивать число испытаний N до бесконечности, то заметим, что относительная частота события А стремится к какому-то определенному числу, которое и называется вероятностью события А и обозначается Р(А). Математически это обозначается:

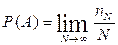
Так как n_N≥0, то Р(А) ≥0 и т.к. n_N≤N, то Р(А) ≤1, т.е. значение вероятности может находиться в пределах 0≤Р(А) ≤1.

Экспериментально это проверить нельзя, т.к. на практике невозможно провести бесконечное количество испытаний.

Далее следует классическое определение вероятности по Лапласу, которое пришло к нам из области азартных игр, где теория вероятностей применялась для определения перспективы выигрыша.

Пусть испытание имеет n возможных исходов, т.е. отдельных событий, могущих появиться в результате данного испытания; причем при каждом повторении испытания возможен один и только один из этих исходов. Таким образом, все n исходов несовместимы. Кроме того, по условиям испытаний нет никаких оснований предполагать, что один из исходов появляется чаще других, т.е. все исходы являются равновозможными.

Допустим теперь, что при n равновозможных исходах интерес представляет только некоторое событие А, появляющееся при каждом из m исходов и не повторяющееся при остальных n-m исходах. Тогда принято говорить, что в данном испытании имеется n случаев, из которых m благоприятствуют появлению события А.

Вероятность события А в такой схеме равна отношению числа случаев, благоприятствующих события А, к общему числу всех равновозможных несовместимых случаев:

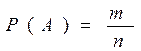
2. В процессе проведения исследований методами математической статистики описывается или измеряется общий признак объектов исследования (спортсменов, например). В результате такого описания или измерения получается статистическая совокупность.

Если статистическая совокупность получена в результате выборочного исследования, то она называется выборочной совокупностью или выборкой.

Под генеральной совокупностью подразумевается совокупность всех возможных значений признака в данном исследовании.

Важнейшая характеристика выборки – объем выборки, т.е. число элементов в ней. Объем выборки принято обозначать символом n.

Генеральную совокупность мысленно можно представить так: это все объекты наблюдения (например, спортсмены), которые обладают теми же свойствами, что и объекты выборки.

Один из центральных вопросов статистики: как обобщить результаты, полученные на выборке, на всю генеральную совокупность?

3. Предметом математической статистики является анализ результатов массовых, повторяющихся измерений. Результаты таких измерений всегда более или менее отличаются друг от друга. Даже если измеряется тот же самый объект в неизменных условиях, нельзя получить одинаковые данные. Из-за многочисленности причин, не поддающихся контролю и варьирующих от одного измерения к другому, результаты измерений всегда претерпевают случайное рассеивание. Аналогичное рассеивание бывает при однотипных измерениях в группе однородных объектов (например, измерения высоты прыжка у группы школьников одного класса). Хотя результат каждого отдельного измерения при случайном рассеивании заранее предсказать нельзя, это не означает, что мы имеем дело с полным хаосом. Массовые изменения однородных объектов, обладающих качественной общностью, обнаруживают определенные закономерности. Математическая статистика создает методы выявления этих закономерностей. Выделяют три основных этапа статистических исследований.

1) Статистическое наблюдение. Представляет собой планомерный, научно обоснованный сбор данных, характеризующих изучаемый объект. Оно должно удовлетворять следующим требованиям:

а) объекты наблюдения (испытуемые) должны быть одинаковыми (однородными) с точки зрения их свойств (квалификация, специализация, возраст, стаж работы и др.);

б) число объектов наблюдения должно быть достаточным, чтобы можно было выявить закономерности и обобщить их свойства.

2) Статистические сводка и группировка. Они являются важной подготовительной частью к статистическому анализу данных. Этот этап предусматривает:

а) систематизацию (группировку) данных;

б) оформление определенных статистических таблиц.

3) Анализ статистического материала. Это завершающий этап статистического исследования. Его проводят с использованием соответствующих математико-статистических методов.

Контрольные вопросы для самопроверки:

1. Что изучает теория вероятностей?

2. Дайте определения случайного события, случайной величины.

3. Дискретные и непрерывные случайные величины.

4. Что такое вероятность?

5. Статистическое определение вероятности.

6. Классическое определение вероятности.

7. Генеральная и выборочная совокупность. Объём выборки.

8. Что изучает математическая статистика?

9. Этапы статистического обследования.

Литература:

1. Основы математической статистики. Уч. пособие для ин-тов физической культуры (под общ. ред. В.С. Иванова). – М.: Физкультура и спорт, 1990. – С. 6 – 12.

2. Рукавицына С.Л., Волков Ю.О., Солтанович Л.Л. Спортивная метрология. Проверка эффективности методики тренировки с применением методов математической статистики. Практикум для студентов БГУФК. – Минск: БГУФК, 2006. – С. 21 – 22.