Понятие дифференциала
Пусть функция y = f(x) дифференцируема при некотором значении переменной x . Следователь-но, в точке x существует конечная производная 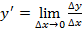 .Тогда по определению предела функции разность
.Тогда по определению предела функции разность 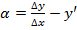 является бесконечно малой величиной при
является бесконечно малой величиной при 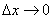 . Выразив из этого равенства приращение функции, получим
. Выразив из этого равенства приращение функции, получим
 (1)
(1)
(величина y  не зависит от
не зависит от 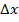 , т. е. остаётся постоянной при
, т. е. остаётся постоянной при  ).
).
Если y’ 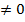 , то в правой части равенства (1) первое слагаемое
, то в правой части равенства (1) первое слагаемое 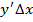 линейно относительно
линейно относительно 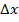 . Поэтому при
. Поэтому при  оно является бесконечно малой того же порядка малости, что и
оно является бесконечно малой того же порядка малости, что и 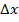
. Второе слагаемое  - бесконечно малая более высокого порядка малости, чем первое, так как их отношение
- бесконечно малая более высокого порядка малости, чем первое, так как их отношение 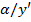 стремится к нулю при
стремится к нулю при  .
.
Поэтому говорят, что первое слагаемое формулы (1) является главной, линейной относительно 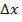 частью приращения функции; чем меньше
частью приращения функции; чем меньше 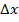 , тем большую долю приращения составляет эта часть. Поэтому при малых значениях
, тем большую долю приращения составляет эта часть. Поэтому при малых значениях 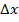 (и при y’
(и при y’ 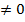 ) приращение функции можно приближенно заменить его главной частью y’
) приращение функции можно приближенно заменить его главной частью y’ 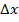 , т.е
, т.е
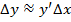 (2)
(2)
Эту главную часть приращения функции называют дифференциалом данной функции в точке x и обозначают dy или df(x).
Следовательно, dy=y’ 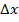 или df(x)=f’(x)
или df(x)=f’(x) 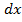 (3)
(3)
Итак, дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной.
Геометрический смысл дифференциала.
Дифференциал функции y = f(x) равен приращению ординаты касательной, проведённой к графику этой функции в точке (x; y), при изменении x на величину 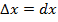 .
.
Поскольку производная 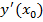 -- это угловой коэффициент
-- это угловой коэффициент 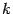 касательной к графику функции при x=
касательной к графику функции при x= 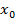 , то дифференциал
, то дифференциал 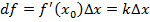 - это приращение ординаты Y точки касательной
- это приращение ординаты Y точки касательной
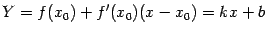
к графику функции y=f(x), когда абсцисса точки касательной получает приращение  :
:
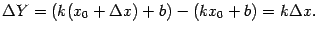
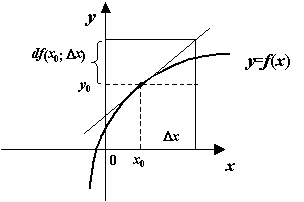
Рис.1Дифференциал равен приращению ординаты касательной
Примеры Найти дифференциалы функций:
1) y= 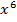 2) y=
2) y= 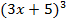 3) y=lnx 4) y=ln(
3) y=lnx 4) y=ln( 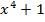 )
)
Решение.
Применяя правила дифференцирования степенной и логарифмической функций,
находим:
1) dy=6 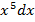 ; 2) dy=3
; 2) dy=3 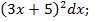 3) dy=
3) dy= 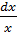 ; 4) dy=
; 4) dy= 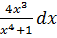
Свойства дифференциала
Дифференциал обладает свойствами, аналогичными свойствам производной:
dc=0 (С – постоянная величина)
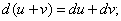
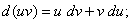

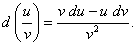
Дата добавления: 2015-08-11; просмотров: 1298;
