Применение дифференциала в приближенных вычислениях
Установленное приближенное равенство 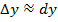 позволяет использовать дифференциал для приближенных вычислений значений функции.
позволяет использовать дифференциал для приближенных вычислений значений функции.
Запишем приближенное равенство более подробно.
Так как 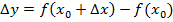 , a dy=f
, a dy=f 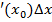 , то f(
, то f( 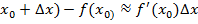 или
или
f( 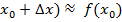 ,+
,+ 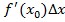 (4)
(4)
Пример 1.
Пользуясь понятием дифференциала, вычислить приближенно ln 1,01.
Решение. Число ln 1,01 является одним из значений функции y = ln x . Формула (4) в данном случае примет вид
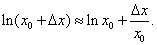 Положим
Положим 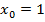 , тогда
, тогда 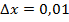
Следовательно, ln(1.01)=ln(1+0.01) 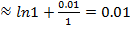 , что является очень хорошим приближением: табличное значение ln 1,01 = 0,0100.
, что является очень хорошим приближением: табличное значение ln 1,01 = 0,0100.
Пример 2.
Пользуясь понятием дифференциала, вычислить приближенно 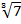 . Оценить точность полученного результата.
. Оценить точность полученного результата.
Решение. Рассмотрим функцию 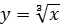 . Её производная равна y
. Её производная равна y  =
= 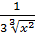 , а формула (4) примет вид
, а формула (4) примет вид
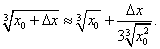
Здесь удобно предварительно представить под корнем 7=8-1 и вынести из под корня число 2,
приняв 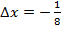
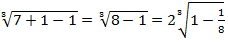 =
= 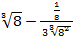 =2 -
=2 - 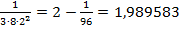
Принимая табличное значение корня 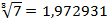 , )абсолютная и относительная погрешности приближенного значения равны:
, )абсолютная и относительная погрешности приближенного значения равны:
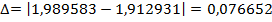
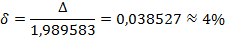
Дата добавления: 2015-08-11; просмотров: 2362;
